如图,已知菱形ABCD的对角线相交于点O,延长AB至点E,使BE=AB,连结CE.
(1)求证:BD=EC;
(2)若∠E=50°,求∠BAO的大小.
如图,在活动课上,小明和小红合作用一副三角板来测量学校旗杆的高度.已知小明的眼睛与地面的距离(AB)是1.7m,他调整自己的位置,设法使得三角板的一条直角边保持水平,且斜边与旗杆顶端M在同一条直线上,测得旗杆顶端M的仰角为45°;小红的眼睛与地面的距离(CD)是1.5m,用同样的方法测得旗杆顶端M的仰角为30°.两人相距28米且位于旗杆两侧(点B、N、D在同一条直线上).求出旗杆MN的高度.(参考数据: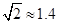 ,
,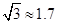 ,结果保留整数)
,结果保留整数)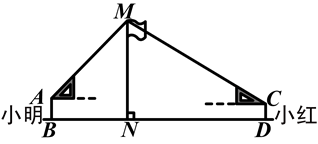
钓鱼岛是中国固有领土,为测量钓鱼岛东西两端A、B的距离,如图,我勘测飞机在距海平面垂直高度为1公里的点C处,测得端点A的俯角为45°,然后沿着平行于AB的方向飞行3.2公里到点D,并测得端点B的俯角为37°.求钓鱼岛两端AB的距离.(结果精确到0.1公里,参考数据:sin37°≈0.60,cos37°≈0.80,tan37°≈0.75, )
)
如图,在电线杆上的C处引拉线CE,CF固定电线杆.拉线CE和地面成60°角,在离电线杆6米处安置测角仪AB,在A处测得电线杆上C处的仰角为30°.已知测角仪AB的高为1.5米,求拉线CE的长.(结果保留根号)
(贵州遵义)如图,一楼房AB后有一假山,其坡度 ,山坡坡面上E点处有一休息亭,测得假山坡脚C与楼房水平距离BC=25米,与亭子距离CE=20米.小丽从楼房顶测得E点的俯角为45°,求楼房AB的高.(注:坡度i是指坡面的铅直高度与水平宽度的比)
,山坡坡面上E点处有一休息亭,测得假山坡脚C与楼房水平距离BC=25米,与亭子距离CE=20米.小丽从楼房顶测得E点的俯角为45°,求楼房AB的高.(注:坡度i是指坡面的铅直高度与水平宽度的比)
(广西桂林)中国“蛟龙”号深潜器目前最大深潜极限为7062.68米,某天该深潜器在海面下1800米处作业(如图),测得正前方海底沉船C的俯角为45°,该深潜器在同一深度向正前方直线航行2000米到B点,此时测得海底沉船C的俯角为60°.
(1)沉船C是否在“蛟龙”号深潜极限范围内?并说明理由;
(2)由于海流原因,“蛟龙”号需在B点处马上上浮,若平均垂直上浮速度为2000米/时,求“蛟龙”号上浮回到海面的时间.