已知:如图14,⊙A与 轴交于C、D两点,圆心A的坐标为(1,0),⊙A的半径为
轴交于C、D两点,圆心A的坐标为(1,0),⊙A的半径为 ,过点C作⊙A的切线交
,过点C作⊙A的切线交 轴于点B(-4,0)
轴于点B(-4,0) .
.
(1)求切线BC的解析式;
(2)若点P是第一象限内⊙A上的一点,过点P作⊙A的切线与直线BC相交于点G,且∠CGP=120°,求点G的坐标.
如图,在 中,
中,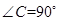 ,
, 平分
平分 交
交 于
于 ,点
,点 在
在 上,以
上,以 为半径的圆,交
为半径的圆,交 于
于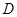 ,交
,交 于
于 ,且点
,且点 在⊙
在⊙ 上,连结
上,连结 ,切⊙
,切⊙ 于点
于点

求证
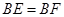
若
 ,求⊙
,求⊙ 的半径
的半径
若从矩形一边上的点到对边的视角是直角,即称该点是直角点。例如,如图的矩形 中,点
中,点 在
在 边上,连接
边上,连接 ,
,
 ,则点
,则点 为直角点。若点
为直角点。若点 分别为矩形
分别为矩形 的边
的边 上的直角点,且
上的直角点,且 ,
, ,则
,则 的长为
的长为
以坐标原点为圆心,1为半径的圆分别交x,y轴的正半轴于点A,B.(1)如图一,动点P从点A处出发,沿x轴向右匀速运动,与此同时,动点Q从点B处出发,沿圆周按顺时针方向匀速运动.若点Q的运动速度比点P的运动速度慢,经过1秒后点P运动到点(2,0),此时PQ恰好是
 的切线,连接OQ. 求
的切线,连接OQ. 求 的大小;
的大小;
(2)若点Q按照(1)中的方向和速度继续运动,点P停留在点(2,0)处不动,求点Q再经过5秒后直线PQ被
 截得的弦长.
截得的弦长.
将一块三角板的直角顶点放在正方形ABCD的对角线交点位置,两边与对角线重合如图甲,将这块三角板绕直角顶点顺时针方向旋转(旋转角小于90°)如图乙.
⑴试判断△ODE和△OCF是否全等,并证明你的结论.
⑵若正方形ABCD的对角线长为10,试求三角板和正方形重合部分的面积.
已知 是⊙
是⊙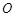 的直径,
的直径,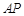 是⊙
是⊙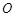 的切线,
的切线, 是切点,
是切点, 与⊙
与⊙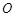 交于点
交于点 .
.(1)如图①,若
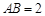 ,
, ,求
,求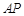 的长(结果保留根号);
的长(结果保留根号);(2)如图②,若
 为
为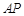 的中点,求证:直线
的中点,求证:直线 是⊙
是⊙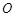 的切线.
的切线.