如图15,抛物线 与
与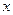 轴交于
轴交于 两点,与
两点,与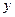 轴交于点
轴交于点 ,连结
,连结 ,若
,若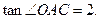
(1)求抛物线对应的二次函数的解析式;
(2)在抛物线的对称轴 上是否存在点
上是否存在点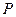 ,使
,使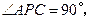 若存在,求出点
若存在,求出点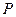 的坐标;若不存在,请说明理由;
的坐标;若不存在,请说明理由;
(3)如图16所示,连结 ,
, 是线段
是线段 上(不与
上(不与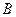 、
、 重合)的一个动点.过点
重合)的一个动点.过点 作直线
作直线 ,交抛物线于点
,交抛物线于点 ,连结
,连结 、
、 ,设点
,设点 的横坐标为
的横坐标为 .当t为何值时,
.当t为何值时, 的面积最大?最大面积为多少?
的面积最大?最大面积为多少?
有一块边长为24米的正方形绿地,如图所示,在绿地旁边B处有健身器材,由于居住在A处的居民践踏了绿地,小明想在A处树立一个标牌“少走▇米,踏之何忍?”请你计算后帮小明在标牌的▇填上适当的数字.
一高层住宅发生火灾,消防车立即赶到距大厦6米处(车尾到大厦墙面),升起云梯到火灾窗口,已知云梯长15米,云梯底部距地面2米,问发生火灾的住户窗口距地面多高?(精确到0.01)
直角三角形ABC中,∠C=90°,CD⊥AB于D,AC=12,BC=16,求AD.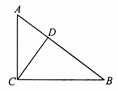
如图甲,四边形ABCD是等腰梯形,AB∥DC,由4个这样的等腰梯形可以拼出图乙所示的平行四边形.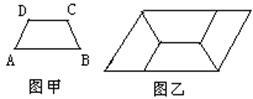
(1)求梯形ABCD四个内角的度数;
(2)试探究四边形ABCD四条边之间存在的等量关系,并说明理由;
图①是等腰梯形ABCD,其中AD∥BC,AB=DC,图②是与图①完全相同的图形.
(1)请你在图①、图②的梯形ABCD中各画一个与△ABD全等但位置不同的三角形,使三角形的各顶点在梯形的边(含顶点)上;
(2)选择(1)中所画的一个三角形说明它与△ABD全等的理由.