下列说法中,正确的是()
| A.所有的有理数都能用数轴上的点表示 |
| B.有理数分为正数和负数 |
| C.符号不同的两个数互为相反数 |
| D.两数相加和一定大于任何一个加数 |
某同学在“百度”搜索引擎中输入“魅力扬州”,能搜索到与之相关的结果个数约为3930000,这个数用科学记数法表示为 ()
| A.0.393×107 | B.393×104 |
| C.39.3×105 | D.3.93×106 |
0.2的倒数是 ()
A.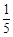 |
B.-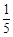 |
C.5 | D.-5 |
在-3,0,4,-5这四个数中,最小的数是 ()
| A.-3 | B.0 | C.4 | D.-5 |
如图,在△ABC中,BD⊥AC,BD=AC,以BC为底边作等腰直角△BEC,连接AE并延长交BD于F点,下列结论:①△AEC≌△DEB ;②AE⊥DE;③DE=DC;④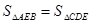 .其中正确的有()个
.其中正确的有()个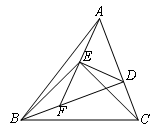
| A.1 | B.2 | C.3 | D.4 |