(本小题满分14分)
三棱 柱
柱 中,
中, 侧棱与底面垂直,
侧棱与底面垂直,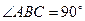 ,
,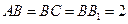 ,
,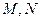 分别是
分别是 ,
, 的中点.
的中点.
(1)求证: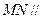 平面
平面 ;
;
(2)求证: 平面
平面 ;
;
(3)求二面角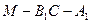 的余弦值.
的余弦值.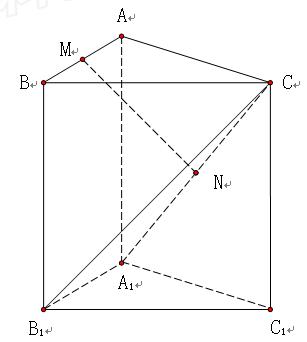
某车间为了规定工时定额,需要确定加工零件所花费的时间,为此作四次试验,得到的数据如下:
| 零件的个数x(个) |
2 |
3 |
4 |
5 |
| 加工的时间y(小时) |
2.5 |
3 |
4 |
4.5 |
(1)已知零件个数与加工时间线性相关,求出y关于x的线性回归方程;
(2)试预测加工10个零件需要多少时间?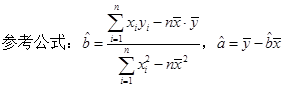
用秦九韶算法求多项式f(x)=2x5-5x4-4x3+3x2-6x+7当x=5时的值.
甲有大小相同的两张卡片,标有数字2、3;乙有大小相同的卡片四张,分别标有1、2、3、4.
(1)求乙随机抽取的两张卡片的数字之和为奇数的概率;
(2)甲、乙分别取出一张卡,比较数字,数字大者获胜,求乙获胜的概率.
用辗转相除法求8251与6105的最大公约数
根据下面的要求,求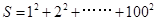 值.
值.
(Ⅰ)请完成执行该问题的程序框图;
(Ⅱ)以下是解决该问题的程序,请完成执行该问题的程序.
