已知函数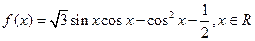 .
.
(Ⅰ) 求函数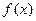 的最小值和最小正周期;
的最小值和最小正周期;
(Ⅱ)已知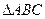 内角
内角 的对边分别为
的对边分别为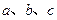 ,且
,且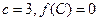 ,若向量
,若向量 与
与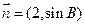 共线,求
共线,求 的值.
的值.
.已知函数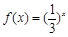 , 其反函数为
, 其反函数为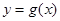
(1) 若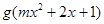 的定义域为
的定义域为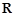 ,求实数
,求实数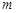 的取值范围;
的取值范围;
(2) 当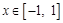 时,求函数
时,求函数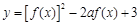 的最小值
的最小值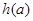 ;
;
(3) 是否存在实数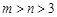 ,使得函数
,使得函数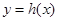 的定义域为
的定义域为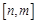 ,值域为
,值域为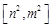 ,若存在,求出
,若存在,求出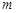 、
、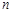 的值;若不存在,则说明理由.
的值;若不存在,则说明理由.
已知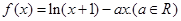
Ⅰ.求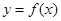 的单调区间;
的单调区间;
Ⅱ.当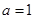 时,求
时,求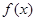 在定义域上的最大值;
在定义域上的最大值;
已知箱中装有4个白球和5个黑球,且规定:取出一个白球的2分,取出一个黑球的1分.现从该箱中任取(无放回,且每球取到的机会均等)3个球,记随机变量X为取出3球所得分数之和.
(Ⅰ)求X的分布列; (Ⅱ)求X的数学期望E(X).
设p:实数x满足 ,其中
,其中 ,命题
,命题 实数x
实数x
满足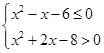
(Ⅰ)若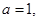 且
且 为真,求实数
为真,求实数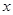 的取值范围;
的取值范围;
(Ⅱ)若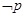 是
是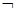
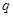 的充分不必要条件,求实数
的充分不必要条件,求实数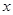 的取值范围.
的取值范围.
(本小题14分)已知函数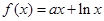
 .
.
(1)若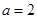 ,求曲线
,求曲线 在
在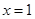 处切线的斜率;
处切线的斜率;
(2)求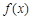 的单调区间;
的单调区间;
(3)设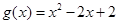 ,若对任意
,若对任意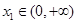 ,均存在
,均存在 ,使得
,使得 ,求
,求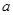 的取值范围。
的取值范围。