(本小题满分12分)
如图,直角梯形ABCD中,AB∥DC,∠DAB=90°,AD=2DC=4,AB=6.动点M以每秒1个单位长的速度,从点A沿线段AB向点B运动;同时点P以相同的速度,从点C沿折线C-D-A向点A运动.当点M到达点B时,两点同时停止运动.过点M作直线l∥AD,与折线A-C-B的交点为Q.点M运动的时间为t(秒).
(1)当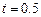 时,求线段
时,求线段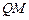 的长;
的长;
(2)点M在线段AB上运动时,是否可以使得以C、P、Q为顶点的三角形为直角三角形,若可以,请直接写出t的值(不需解题步骤);若不可以,请说明理由.
(3)若△PCQ的面积为y,请求y关于出t 的函数关系式及自变量的取值范围;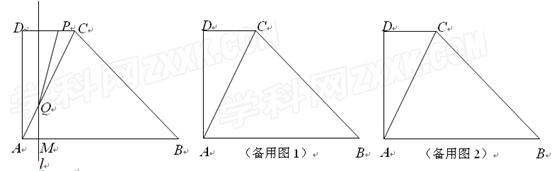
如图,A,B,C,D,E,F,M,N是某公园里的8个独立的景点,D,E,B三个景点之间的距离相等;A,B,C三个景点距离相等.其中D,B,C在一条直线上,E,F,N,C在同一直线上,D,M,F,A也在同一条直线上.游客甲从E点出发,沿E→F→N→C→A→B→M游览,同时,游客乙从D点出发,沿D→M→F→A→C→B→N游览.若两人的速度相同且在各景点游览的时间相同,甲、乙两人谁最先游览完?请说明理由.
如图,矩形ABCD中,AB=4,BC=9,动点Q沿着C→D→A→B的方向运动至点B停止,设点Q运动的路程为x,△QCB的面积为y.
(1)当点Q在CD上运动时,求y与x的关系式;
(2)当点Q在AD上运动时,△QCB的面积改变了吗?请说明理由.
(3)说一说y是怎样随着x的变化而变化的?
如图所示,图象反映的是:张阳从家里跑步去体育场,在那里锻炼了一阵后又走到文具店去买笔,然后走回家,其中x表示时间,y表示张阳离家的距离.根据图象回答下列问题:
(1)体育场离张阳家_________千米;
(2)体育场离文具店_________千米;张阳在文具店逗留了_____分钟;
(3)请计算:张阳从文具店到家的平均速度约是每小时多少千米?
很多代数原理都可以用几何模型解释.现有若干张如图所示的卡片,请拼成一个边长为(2a+b)的正方形(要求画出简单的示意图),并指出每种卡片分别用了多少张?然后用相应的公式进行验证.
“石头、剪刀、布”是民间广为流传的游戏.现在,很多小朋友在玩这个游戏时对此进行了“升级”:喊着“左一刀,右一刀”的口号同时,左右手接连伸出手势,喊“关键时候收一刀”时收回其中一手.假如甲的左右手势分别是“石头”和“剪刀”,乙的左右手势分别是“剪刀”和“布”,双方任意收回一种手势.
(1)可能会出现哪些等可能的结果?
(2)乙赢的概率是多少?