很多代数原理都可以用几何模型解释.现有若干张如图所示的卡片,请拼成一个边长为(2a+b)的正方形(要求画出简单的示意图),并指出每种卡片分别用了多少张?然后用相应的公式进行验证.
如图, , .求证: .
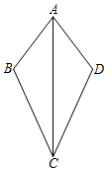
如图,在平行四边形 中,点 是 的中点,点 是 边上的点, ,平行四边形 的面积为 ,由 、 、 三点确定的圆的周长为 .
(1)若 的面积为30,直接写出 的值;
(2)求证: 平分 ;
(3)若 , , ,求 的值.
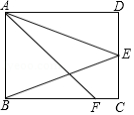
如图,已知 是 的直径, 是 上的点,点 在 的延长线上, .
(1)求证: 是 的切线;
(2)若 , ,求图中阴影部分的面积.
某驻村扶贫小组为解决当地贫困问题,带领大家致富.经过调查研究,他们决定利用当地盛产的甲、乙两种原料开发 、 两种商品.为科学决策,他们试生产 、 两种商品共100千克进行深入研究,已知现有甲种原料293千克,乙种原料314千克,生产1千克 商品,1千克 商品所需要的甲、乙两种原料及生产成本如表所示.
|
甲种原料(单位:千克) |
乙种原料(单位:千克) |
生产成本(单位:元) |
|
|
商品 |
3 |
2 |
120 |
|
商品 |
2.5 |
3.5 |
200 |
设生产 种商品 千克,生产 、 两种商品共100千克的总成本为 元,根据上述信息,解答下列问题:
(1)求 与 的函数解析式(也称关系式),并直接写出 的取值范围;
(2) 取何值时,总成本 最小?
已知二次函数 的图象经过 , 两点.
(1)求 , 的值.
(2)二次函数 的图象与 轴是否有公共点?若有,求公共点的坐标;若没有,请说明情况.