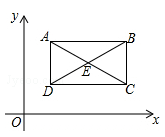
如图,在平行四边形中,点是的中点,点是边上的点,,平行四边形的面积为,由、、三点确定的圆的周长为.
(1)若的面积为30,直接写出的值;
(2)求证:平分;
(3)若,,,求的值.
现正是闽北特产杨梅热销的季节,某水果零售商店分两批次从批发市场共购进杨梅40箱,已知第一、二次进货价分别为每箱50元、40元,且第二次比第一次多付款700元.
(1)设第一、二次购进杨梅的箱数分别为a箱、b箱,求a,b的值;
(2)若商店对这40箱杨梅先按每箱60元销售了x箱,其余的按每箱35元全部售完.
①求商店销售完全部杨梅所获利润y(元)与x(箱)之间的函数关系式;
②当x的值至少为多少时,商店才不会亏本.
(注:按整箱出售,利润=销售总收入﹣进货总成本)
如图,在平面直角坐标系中,已知抛物线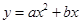 的对称轴为
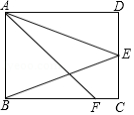
的对称轴为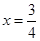 ,且经过点A(2,1),点P是抛物线上的动点,P的横坐标为m(0<m<2),过点P作PB⊥x轴,垂足为B,PB交OA于点C,点O关于直线PB的对称点为D,连接CD,AD,过点A作AE⊥x轴,垂足为E.
,且经过点A(2,1),点P是抛物线上的动点,P的横坐标为m(0<m<2),过点P作PB⊥x轴,垂足为B,PB交OA于点C,点O关于直线PB的对称点为D,连接CD,AD,过点A作AE⊥x轴,垂足为E.
(1)求抛物线的解析式;
(2)填空:①用含m的式子表示点C,D的坐标:C( , ),D( , );
②当m= 时,△ACD的周长最小;
(3)若△ACD为等腰三角形,求出所有符合条件的点P的坐标.
如图.抛物线y=x2-4x与x轴交于O,A两点,P为抛物线上一点,过点P的直线y="x+" m与对称轴交于点Q.
( 1 )这条抛物线的对称轴是 ,直线PQ与x軸所夹锐角的度数是 ;
(2)若两个三角形面积满足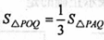 ,求m的値;
,求m的値;
(3)当点P在x軸下方的抛物线上时.过点C(2,2)的直线AC与直线PQ交于点D,求:
PD+DQ的最大值;②PD·DQ的最大值.
已知点A(-2,n)在抛物线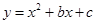 上.
上.
(1)若b=1,c=3,求n的值;
(2)若此抛物线经过点B(4,n),且二次函数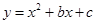 的最小值是-4,请画出点P(
的最小值是-4,请画出点P(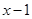 ,
, )的纵坐标随横坐标变化的图象,并说明理由.
)的纵坐标随横坐标变化的图象,并说明理由.
如图,在平面直角坐标系中,点A(2,n),B(m,n)(m>2),D(p,q)(q<n),点B,D在直线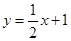 上.四边形ABCD的对角线AC,BD相交于点E,且AB∥CD,CD=4,BE=DE,△AEB的面积是2.求证:四边形ABCD是矩形.
上.四边形ABCD的对角线AC,BD相交于点E,且AB∥CD,CD=4,BE=DE,△AEB的面积是2.求证:四边形ABCD是矩形.