如图．抛物线y=x2-4x与x轴交于O，A两点，P为抛物线上一点,过点P的直线y="x+" m与对称轴交于点Q．
（ 1 ）这条抛物线的对称轴是 ，直线PQ与x軸所夹锐角的度数是 ；
（2）若两个三角形面积满足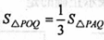
，求m的値；
（3）当点P在x軸下方的抛物线上时．过点C（2，2）的直线AC与直线PQ交于点D，求：
PD+DQ的最大值；②PD·DQ的最大值．
已知：如图，AD，BC相交于点O，OA=OD，AB∥CD．
求证：AB=CD．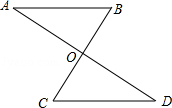
已知抛物线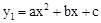
a≠0）的对称轴是直线l，顶点为点M．若自变量x和函数值y1的部分对应值如下表所示：
| x |
… |
―1 |
0 |
3 |
… |
|
… |
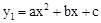0 |
 |
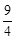0 |
… |
（1）求y1与x之间的函数关系式；
（2）若经过点T（0，t）作垂直于y轴的直线l′，A为直线l′上的动点，线段AM的垂直平分线交直线l于点B，点B关于直线AM的对称点为P，记P（x，y2）．
①求y2与x之间的函数关系式；
②当x取任意实数时，若对于同一个x，有y1＜y2恒成立，求t的取值范围．
甲、乙两商场以同样价格出售同样的商品，并且又各自推出不同的优惠方案：在甲商场累计购物超过100元后，超出100元的部分按90%收费；在乙商场累计购物超过50元后，超出50元的部分按95%收费，设小红在同一商场累计购物x元，其中x＞100．
（1）根据题题意，填写下表（单位：元）
| 累计购物实际花费 |
130 |
290 |
… |
x |
| 在甲商场 |
127 |
… |
||
| 在乙商场 |
126 |
… |
（2）当x取何值时，小红在甲、乙两商场的实际花费相同？
（3）当小红在同一商场累计购物超过100元时，在哪家商场的实际花费少？
天塔是天津市的标志性建筑之一，某校数学兴趣小组要测量天塔的高度，如图，他们在点A处测得天塔最高点C的仰角为45°，再往天塔方向前进至点B处测得最高点C的仰角为54°，AB=112m，根据这个兴趣小组测得的数据，计算天塔的高度CD（tan36°≈0.73，结果保留整数）．
已知直线l与⊙O，AB是⊙O的直径，AD⊥l于点D．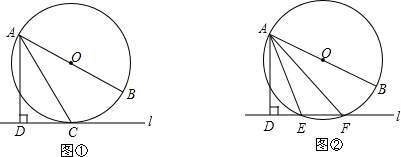
（1）如图①，当直线l与⊙O相切于点C时，若∠DAC=30°，求∠BAC的大小；
（2）如图②，当直线l与⊙O相交于点E、F时，若∠DAE=18°，求∠BAF的大小．