(本小题满分12分)在△ABC中,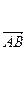 ·
·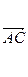 =1,
=1,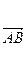 ·
·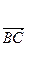 =-3
=-3
(I)求△ABC的边AB的长
(II)求 的值
的值
已知: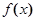 是一次函数,其图像过点
是一次函数,其图像过点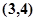 ,且
,且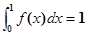 ,求
,求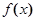 的解析式。
的解析式。
已知复数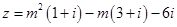 ,则当m为何实数时,复数z是
,则当m为何实数时,复数z是
(1)实数;(2)虚数;(3)纯虚数;(4)零;(5)对应的点在第三象限
如图所示,流程图给出了无穷等差整数列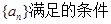 ,
,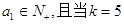 时,输出的
时,输出的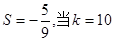 时,输出的
时,输出的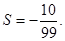 (其中d为公差)
(其中d为公差)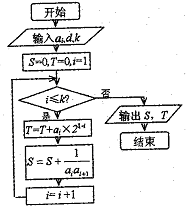
(I)求数列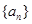 的通项公式;
的通项公式;
(II)是否存在最小的正数m,使得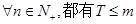 成立?若存在,求出m的值,若不存在,请说明理由。
成立?若存在,求出m的值,若不存在,请说明理由。
已知点B(0,1),点C(0,—3),直线PB、PC都是圆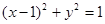 的切线(P点不在y轴上).
的切线(P点不在y轴上).
(I)求过点P且焦点在x轴上抛物线的标准方程;
(II)过点(1,0)作直线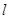 与(I)中的抛物线相交于M、N两点,问是否存在定点R,使
与(I)中的抛物线相交于M、N两点,问是否存在定点R,使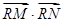 为常数?若存在,求出点R的坐标与常数;若不存在,请说明理由。
为常数?若存在,求出点R的坐标与常数;若不存在,请说明理由。
已知函数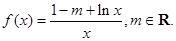
(I)若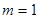 ,判断函数在定义域内的单调性;
,判断函数在定义域内的单调性;
(II)若函数在 内存在极值,求实数m的取值范围。
内存在极值,求实数m的取值范围。