(本小题满分12分)
设数列{an}的首项a1∈(0,1),an+1= (n∈N+)
(n∈N+)
(I)求{an}的通项公式
(II)设bn=an ,判断数列{bn}的单调性,并证明你的结论
,判断数列{bn}的单调性,并证明你的结论
已知{an}为等差数列,且a1+a3=8,a2+a4=12.
(1){an}的通项公式;
(2)记{an}的前n项和为Sn,若a1,ak,Sk+2成等比数列,求正整数k的值.
已知数列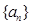 的前
的前 项和
项和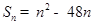 。
。
(1)求数列的通项公式;
(2)求 的最大或最小值。
的最大或最小值。
甲、乙两位学生参加数学竞赛培训。现分别从他们在培训期间参加的若干次预赛成绩中随机抽取8次,记录如下:
甲 82 81 79 78 95 88 93 84
乙 92 95 80 75 83 80 90 85
(1)用茎叶图表示这两组数据,并指出两组数据的中位数。
(2)从平均数、方差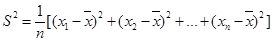 考虑,你认为哪位学生更稳定?请说明理由。
考虑,你认为哪位学生更稳定?请说明理由。
(本小题14分)已知直线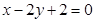 经过椭圆
经过椭圆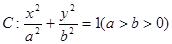 的左顶点A和上顶点D,椭圆
的左顶点A和上顶点D,椭圆 的右顶点为
的右顶点为 ,点
,点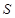 是椭圆
是椭圆 上位于
上位于 轴上方的动点,直线
轴上方的动点,直线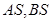 与直线
与直线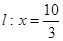 分别交于
分别交于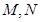 两点。
两点。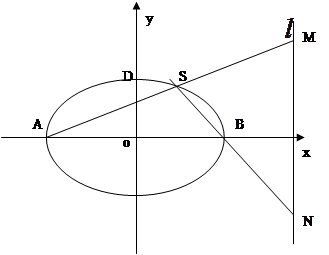
(I)求椭圆 的方程;
的方程;
(Ⅱ)求线段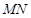 的长度的最小值;
的长度的最小值;
(Ⅲ)当线段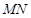 的长度最小时,在椭圆
的长度最小时,在椭圆 上是否存在这样的点
上是否存在这样的点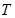 ,使得
,使得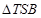 的面积为
的面积为 ?若存在,确定点
?若存在,确定点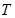 的个数,若不存在,说明理由。
的个数,若不存在,说明理由。
(本小题12分)某工厂有工人1000名,其中250名工人参加过短期培训(称为A类工人),另外750名工人参加过长期培训(称为B类工人).现用分层抽样方法(按A类,B类分二层)从该工厂的工人中共抽查100名工人,调查他们的生产能力(生产能力指一天加工的零件数).从A类工人中抽查结果和从B类工人中的抽查结果分别如下表1和表2
表1:
| 生产能力分组 |
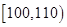 |
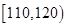 |
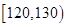 |
 |
 |
| 人数 |
4 |
8 |
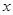 |
5 |
3 |
表2:
| 生产能力分组 |
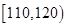 |
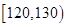 |
 |
 |
| 人数 |
6 |
y |
36 |
18 |
(1)先确定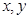 ,再在答题纸上完成下列频率分布直方图。就生产能力而言,A类工人中个体间的差异程度与B类工人中个体间的差异程度哪个更小?(不用计算,可通过观察直方图直接回答结论)(注意:本题请在答题卡上作图)
,再在答题纸上完成下列频率分布直方图。就生产能力而言,A类工人中个体间的差异程度与B类工人中个体间的差异程度哪个更小?(不用计算,可通过观察直方图直接回答结论)(注意:本题请在答题卡上作图)
(2)分别估计 类工人和
类工人和 类工人生产能力的众数、中位数和平均数。(精确到0.1)
类工人生产能力的众数、中位数和平均数。(精确到0.1)