(10分)如图所示,斜面倾角为θ,质量为m的滑块距挡板P为s0,以初速度v0。沿斜面上滑。滑块与斜面间的动摩擦因数为μ,滑块所受摩擦力小于滑块沿斜面的下滑力。若滑块每次与挡板相碰均无机械能损失。问滑块经过的路程有多大?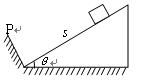
半径为R的玻璃圆柱体,截面如图所示,圆心为O,在同一截面内,两束相互垂直的单色光射向圆柱面的A、B两点,其中一束沿AO方向,∠AOB=30°,若玻璃对此单色光的折射率n= .
.
①试作出两条光线从射入到第一次射出的光路途径,并求出B光第一次射出圆柱面时的折射角。(当光线射向柱面时,如有折射光线则不考虑反射光线)
②求两条光线经圆柱体后第一次射出的光线的交点(或延长线的交点)与A点的距离。
如图所示, 一圆柱形绝热容器竖直放置, 通过绝热活塞封闭着摄氏温度为t1的理想气体, 活塞的质量为m, 横截面积为S, 与容器底部相距h1.现通过电热丝给气体加热一段时间, 使其温度上升到t2, 若这段时间内气体吸收的热量为Q, 已知大气压强为p0, 重力加速度为g, 求:
①气体的压强.
②这段时间内活塞上升的距离是多少?
③这段时间内气体的内能变化了多少?
如图(a)所示,一边长L=2.5m,质量m=0.5kg的正方形金属线框,放在光滑绝缘的水平面上,整个装置放在方向竖直向上、磁感应强度B=1.6T的匀强磁场中,它的一边与磁场的边界MN重合。在水平力F作用下由静止开始向左运动,经过5s线框被拉出磁场。测得金属线框中的电流随时间变化的图像如图(b)所示,在金属线框被拉出的过程中,
(1)求通过线框导线截面的电量及线框的电阻;
(2)写出水平力F随时间t变化的表达式;
(3)已知在这5s内力F做功3.58J,那么此过程中,线框产生的焦耳热为是多少?
直角坐标系中,第四象限有与X轴正方向相同的匀强电场;另一匀强电场在第一象限,其方向与Y轴正方向相同,在第二和第三象限其电场方向与Y轴负方向相同。同时在X轴的正半轴有垂直纸面向里的匀强磁场。如图所示,现一质量m、电量q的电荷从A点以速度v,与Y轴正向成30°夹角进入该直角坐标系中。先做直线运动,接着在第一象限恰好做匀速圆周运动,且与X轴垂直相交于B点,后在第二象限发生偏转与X轴负半轴交于C点。已知重力加速度为g。求: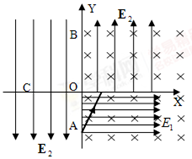
(1)第四象限的电场强度大小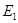 与第二象限的电场强度大小
与第二象限的电场强度大小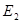 的比值?
的比值?
(2)B点的纵坐标?
(3)电荷从B点运动到C的时间?
一轻质弹簧竖直固定在地面上,上面连接一个质量为m1=1kg的物体,平衡时物体离地面0.9m,弹簧所具有的弹性势能为0.5J。现在在距物体m1正上方高为0.3m处有一个质量为m2=1kg的物体自由下落后与弹簧上物体m1碰撞立即合为一体,一起向下压缩弹簧。当弹簧压缩量最大时,弹簧长为0.6m。求(g取10m/s2):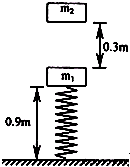
①碰撞结束瞬间两物体的动能之和是多少?
②弹簧长为0.6m时弹簧的弹性势能大小?