已知圆
，点P是直线
上的一动点，过点P作圆M的切线PA，PB，切点为A，B．
（1）当切线PA的长度为
时，求点P的坐标；
（2）若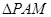
的外接圆为圆N，试问：当P在直线
上运动时，圆N是否过定点？若存在，求出所有的定点的坐标；若不存在，说明理由．
（3）求线段AB长度的最小值．
如图，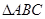
的顶点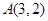
，
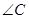的平分线CD所在直线方程为
，AC边上的高BH所在直线方程为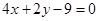
．
（1）求顶点C的坐标；
（2）求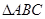的面积．
已知
为数列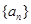
的前n项和，且
，
．
（1）求数列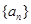的通项公式；
（2）设
，求数列
的前n项和
．
，
，
．
（1）比较
与
的大小；
（2）解关于x的不等式：
．
椭圆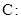
（
）的上顶点为
，
是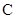
上的一点，以
为直径的圆经过椭圆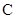的右焦点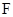
．
（1）求椭圆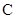的方程；
（2）动直线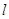
与椭圆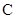有且只有一个公共点，问：在
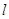轴上是否存在两个定点，它们到直线的距离之积等于
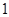？如果存在，求出这两个定点的坐标；如果不存在，说明理由．
数
.
在点
处的切线斜率为4，求实
数
的值；
上是单调函数，求实数