在平面上有且只有4个点,这4个点中有一个独特的性质:连结每两点可得到6条线段,这6条线段有且只有两种长度.我们把这四个点称作准等距点.例如正方形ABCD的四个顶点(如图1),有AB=BC=CD=DA,AC=BD.其实满足这样性质的图形有很多,如图2中A、B、C、O四个点,满足AB=BC=CA,OA=OB=OC;如图3中A、B、C、O四个点,满足OA=OB=OC=BC,AB=AC.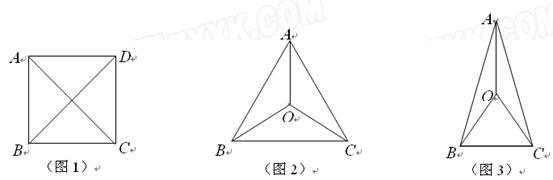
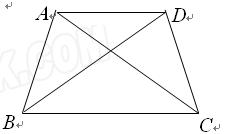
(1)如图,若等腰梯形ABCD的四个顶点是准等距点,且AD∥BC.
①写出相等的线段(不再添加字母);
②求∠BCD的度数.
(2)请再画出一个四边形,使它的四个顶点为准等距点,并写出相等的线段.
在长方形纸片内部裁剪出一个长方形,尺寸如图所示.
(1)用含有a、b、x的代数式表示图中阴影部分的面积:;
(2)当 ,
, 时,求此时阴影部分的面积.
时,求此时阴影部分的面积.
已知:直线AB与直线CD相交于点O,∠BOC= ,
,

(1)如图1,若EO⊥AB,求∠DOE的度数;
(2)如图2,若EO平分∠AOC,求∠DOE的度数.
已知:关于x的方程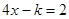 与
与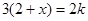 的解相同,求
的解相同,求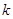 的值及相同的解.
的值及相同的解.
某校七年级举行踢毽比赛,参加的人数是未参加人数的3倍,如果该年级学生减少6人,未参加的学生增加6人,那么参加与未参加比赛的人数之比是2︰1,求该校七年级原有的人数.
已知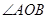 ,
,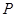 为
为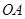 上一点.
上一点.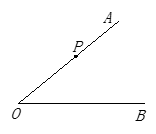
(1)过点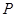 画一条直线
画一条直线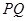 ,使
,使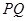 ∥
∥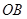 ;
;
(2)过点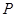 画一条直线
画一条直线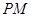 ,使
,使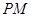 ⊥
⊥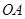 交
交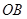 于点
于点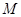 ;
;
(3)若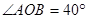 ,则
,则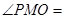 °.
°.