如图,在□ABCD中,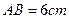 ,
,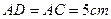 .点
.点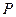 由
由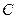 出发沿
出发沿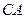 方向匀速运动,速度为
方向匀速运动,速度为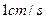 ;同时,线段
;同时,线段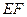 由
由 出发沿
出发沿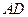 方向匀速运动,速度为
方向匀速运动,速度为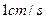 ,交
,交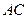 于
于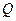 ,连接
,连接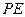 、
、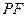 .若设运动时间为
.若设运动时间为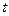 (s)(
(s)(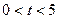 ).解答下列问题:
).解答下列问题:
(1)当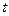 为何值时,
为何值时,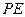 ∥
∥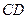 ?并求出此时
?并求出此时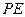 的长;
的长;
(2)试判断△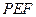 的形状,并请说明理由.
的形状,并请说明理由.
(3)当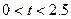 时,
时,
(ⅰ)在上述运动过程中,五边形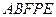 的面积 ▲ (填序号)
的面积 ▲ (填序号)
①变大 ②变小 ③先变大,后变小 
 ④不变
④不变
(ⅱ)设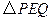 的面积为
的面积为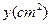 ,求出
,求出 与
与 之间的函数关系式及
之间的函数关系式及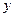 的取值范围.
的取值范围.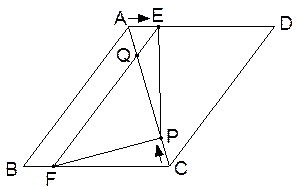
(本题6分)a,b为有理数,如果规定一种新的运算“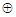 ”,定义:a
”,定义:a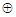 b=a2-ab+a-1,请根据“
b=a2-ab+a-1,请根据“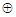 ”的定义计算下列各题:
”的定义计算下列各题:
例如:2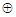 (-5)=
(-5)=
=4-(-10)+2-1=4+10+2-1=15
计算:(1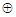 3)
3)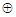 (-3)
(-3)
(本题6分)先化简再求值: ,其中x=1,y=-1.
,其中x=1,y=-1.
在“元旦”期间,小明,小亮等同学随家长一同到我市某景区游玩,下面是买门票时,小明与他爸爸看了票价后的对话:
票价:成人:每张35元; 学生:按成人票价的5折优惠; 团体票(16人以上含16人):按成人票价的a折优惠.
爸爸:大人门票是每张35元,学生门票是5折优惠,我们一共12人,共需350元.
小明:爸爸,等一下,让我算一算,如果按团体票方式买票,还可节省14元.
试根据以上信息,解答以下问题:
(1)小明他们一共去了几个成人?几个学生?
(2)求票价中a的值.
电影院第一排有10个座位,后面一排比紧挨的前面一排多一个座位.
(1)如果某电影院2号厅有6排座位,那么该厅一共有多少个座位?
(2)如果有n排座位,那么该厅第n排有几个座位?该厅最后3排一共有多少个座位?若n为奇数,那么该厅一共有多少个座位?(用含n的代数式表示)
已知: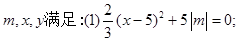
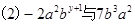 是同类项.求代数式:
是同类项.求代数式: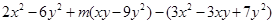 的值。
的值。