(本小题满分12分)设函数 。
。
(1)当 时,求
时,求 的单调区间。
的单调区间。
(2)若 在
在 上的最大值为
上的最大值为 ,求
,求 的值。
的值。
已知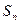 为数列
为数列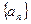 的前
的前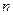 项和,点
项和,点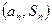 在直线
在直线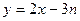 上.
上.
⑴若数列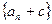 成等比,求常数的值;
成等比,求常数的值;
⑵求数列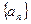 的通项公式;
的通项公式;
⑶数列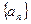 中是否存在三项,它们可以构成等差数列?若存在,请求出一组适合条件的项;
中是否存在三项,它们可以构成等差数列?若存在,请求出一组适合条件的项;
若不存在,请说明理由.
用砖砌墙,第一层(底层)用去了全部砖块的一半多一块,第二层用去了剩下的一半多一块,…依次类推,每一层都用去了上次剩下的砖块的一半多一块,到第十层恰好把砖块用完,问共用了多少块?
设函数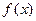 的定义域为
的定义域为 ,当
,当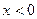 时,
时, ,且对任意的实数
,且对任意的实数 ,有
,有 .
.
⑴求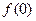 ,判断并证明函数
,判断并证明函数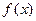 的单调性;
的单调性;
⑵数列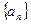 满足
满足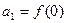 ,且
,且
①求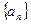 通项公式;
通项公式;
②当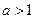 时,不等式
时,不等式 对不小于
对不小于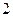 的正整数恒成立,求
的正整数恒成立,求 的取值范围.
的取值范围.
已知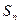 为数列
为数列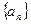 的前
的前 项和,
项和, ,
,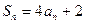 .
.
⑴设数列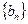 中,
中, ,求证:
,求证: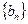 是等比数列;
是等比数列;
⑵设数列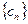 中,
中,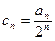 ,求证:
,求证: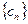 是等差数列;
是等差数列;
⑶求数列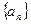 的通项公式及前
的通项公式及前 项和.
项和.
【解题思路】由于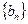 和
和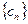 中的项与
中的项与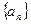 中的项有关,且
中的项有关,且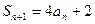 ,可利用
,可利用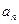 、
、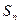 的关系作为切入点.
的关系作为切入点.
已知等差数列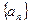 与等比数列
与等比数列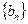 中,
中,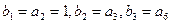 ,求
,求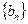 的通项.
的通项.