（本题共3小题，第（1）小题4分，第（2）、（3）小题每小题5分，满分14分）
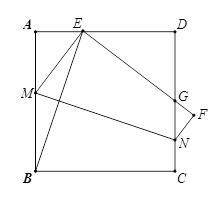
如图，在矩形ABCD中，点E在边AD上，联结BE，∠ABE = 30°，BE = DE，联结BD．点M为线段DE上的任意一点，过点M作MN // BD，与BE相交于点N．
（1）如果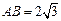
，求边AD的长；
（2）如图1，在（1）的条件下，如果点M为线段DE
的中点，联结CN．过点M作MF⊥CN，垂足为点F，求线段MF的长；
（3）试判断BE、MN、MD这三条线段的长度之间有怎样的数量关系？请证明你的结论．
解不等式组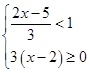
化简
－
．
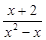如图，已知在Rt△ABC中，∠ABC=90°，∠C=30°，AC=12cm，点E从点A出发沿AB以每秒1cm的速度向点B运动，同时点D从点C出发沿CA以每秒2cm的速度向点A运动，运动时间为t秒（0＜t＜6），过点D作DF⊥BC于点F．
（1）试用含t的式子表示AE、AD的长；
（2）如图①，在D、E运动的过程中，四边形AEFD是平行四边形，请说明理由；
（3）如图②，连接DE，当t为何值时，△DEF为直角三角形？
（4）如图③，将△ADE沿DE翻折得到△A′DE，试问当t为何值时，四边形AEA′D为菱形？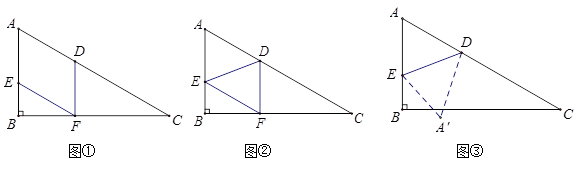
观察下列等式：
①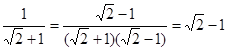
；
②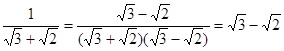
；
③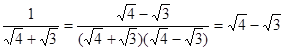
；
……
回答下列问题：
（1）仿照上列等式，写出第n个等式：;
（2）利用你观察到的规律，化简：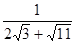
；
（3）计算：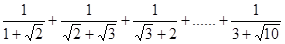
如图，M、N是正方形ABCD边AB、CD上两动点，连接MN，将四边形BCNM沿MN折叠，使点B落在AD边上点E处、点C落在点F.
（1）求证：BE平分∠AEF；
（2）求证：C△EDG=2AB（注：C△EDG表示△EDG的周长）