(本小题满分12分）某企业生产甲、乙两种产品, 根据市场调查与预测, 甲产品
的利润与投资成正比, 其关系如图1, 乙产品的利润与投资的算术平方根成正比, 其关系如
图2 (注: 利润与投资
的单位: 万元).
(Ⅰ) 分别将甲、乙两种产品的利润表示为投资的函数关系式；
(Ⅱ) 该企业筹集了100万元资金投入生产甲、乙两种产品, 问: 怎样分配这100万元资金, 才能使企业获得最大利润, 其最大利润为多少万元？
设函数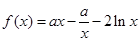
．
（1）若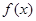
在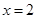
时有极值，求实数
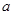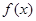的值和的极大值；
（2）若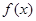在定义域上是增函数,求实数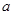的取值范围．
已知椭圆C的两焦点分别为
，长轴长为6，
⑴求椭圆C的标准方程;
⑵已知过点（0，2）且斜率为1的直线交椭圆C于A 、B两点,求线段AB的长度。．
已知
的第五项的二项式系数与第三项的二项式系数的比是
，
(1)求n；
(2)求展开式中常数项．
修建一个面积为
平方米的矩形场地的围墙，要求在前面墙的正中间留一个宽度为2米的出入口，后面墙长度不超过20米，已知后面墙的造价为每米45元，其它墙的造价为每米180元，设后面墙长度为x米，修建此矩形场地围墙的总费用为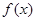
元.
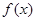（1）求的表达式；
（2）试确定x，使修建此矩形场地围墙的总费用最小，并求出最小总费用.
已知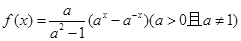
（1）判断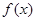
的奇偶性；
（2）讨论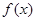的单调性；
（3）当
时，
恒成立，求b的取值范围.