已知 向量
向量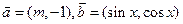 ,
,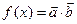 且满足
且满足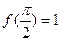 .
.
(1)求函数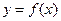 的解析式;
的解析式;
(2)求函数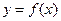 的最大值及其对应的
的最大值及其对应的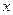 值;
值;
(3)若 ,求
,求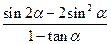 的值.
的值.
已知函数 满足
满足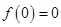 ,且
,且 ,令
,令 .
.
(1)求函数 的表达式;
的表达式;
(2)求函数 的最小值.
的最小值.
已知集合A={x|2a+1≤x≤3a-5},B={x|x<-1,或x>16},分别根据下列条件求实数a的取值范围.
(1)A∩B= ;(2)A⊆(A∩B).
;(2)A⊆(A∩B).
已知A⊆M={x|x2-px+15=0,x∈R},B⊆N={x|x2-ax-b=0,x∈R},又A∪B={2,3,5},A∩B={3},求p,a和b的值.
(本小题满分12分)函数 是定义在
是定义在 上的奇函数,且
上的奇函数,且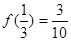 .
.
(1)求实数 ,并确定函数
,并确定函数 的解析式;
的解析式;
(2)用定义证明 在
在 上是增函数;
上是增函数;
(3)写出 的单调减区间,并判断
的单调减区间,并判断 有无最大值或最小值?如有,写出最大值或最小值.(本小问不需说明理由)
有无最大值或最小值?如有,写出最大值或最小值.(本小问不需说明理由)
(本小题满分12分)已知
(1)设 ,求
,求 的最大值与最小值;
的最大值与最小值;
(2)求 的最大值与最小值;
的最大值与最小值;