商场某种商品平均每天可销售30件,每件盈利50元. 为了尽快减少库
存,商场决定采取适当的降价措施. 经调查发现,每件商品每降价1元,商场平均每天可多
售出 2件.设每件商品降价x元. 据此规律,请回答:
(1)商场日销售量增加 件,每件商品盈利 元(用含x的代数式表示);
(2)在上述条件不变、销售正常情况下,每件商品降价多少元时,商场日盈利可达到2100元?
已知:如图,在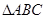 中,
中, 是
是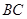 边上的高,
边上的高,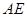 是
是 平分线。求
平分线。求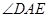 的度数。
的度数。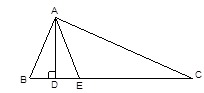
已知, ,
, ,
,
其中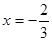 ,
,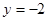 。比较A和B的值的大小。小明说A的值大,
。比较A和B的值的大小。小明说A的值大,
小华说B的值大。请你判断一下,谁的说法正确,为什么?
计算: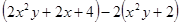


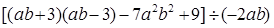
已知正比例函数y=kx经过点A(2,1),如图10所示.求这个正比例函数的关系式.
将这个正比例函数的图像向左平移4个单位,写出在这个平移下,点A、原点O的对应点A/、O/的坐标,求出平移后的直线O/A/所对应的函数关系式.
已知点C的坐标为(-3,0),点P(x,y)为线段O/B上一动点(P与O/、B不重合),设△PCO的面积为S.
①求S与x之间的函数关系式及x的取值范围;
②② 求当S= 时,点P的坐标.
时,点P的坐标.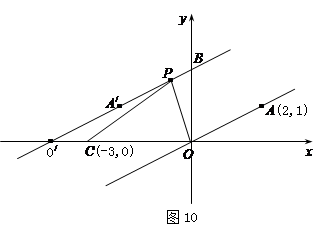
某公司市场营销部的营销员的个人月收入与该营销员每月的销量成一次函数关系,其图象如图8所示. 根据图象提供的信息,解答下列问题:求出营销人员的个人月收入y元与该营销员每月的销售量x万件(x≥0)之间的函数关系式;
该公司营销人员的底薪是(没有销售量时的收入)多少元?
已知该公司营销员李明5月份的销售量为1.2万件,求李明5月份的收入.