(本小题10分)某企业获准生产“上海世博会”纪念徽章,若生产A种款式的纪念徽章125件,B种款式的纪念徽章150件,需生产成本700元;若生产A种款式的纪念徽章100件,B种款式的纪念徽章450件,需生产成本1550元.已知A、B两种纪念徽章的市场零售价分别为2.3元,3.5元.
(1)求A、B两种款式的纪念徽章每个成本是多少元?
(2)随着上海世博会的开幕,为了满足市场的需要,该企业现在每天要生产A、B两种款式的纪念徽章共4500件,若要求每天投入成本不超过1万元,并且每天生产的B种款式的纪念徽章不少于A种款式纪念徽章的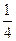 .那么每天最多获利多少元,最少获利多少元?
.那么每天最多获利多少元,最少获利多少元?
如图,在矩形ABCD中,对角线BD的垂直平分线MN与AD相交于点M,与BC相交于点N,连接BM,DN.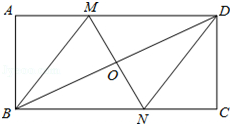
(1)求证:四边形BMDN是菱形;
(2)若AB=4,AD=8,求MD的长.
如图,直角坐标系中,点A的坐标为(1,0),以线段OA为边在第四象限内作等边△AOB,点C为x正半轴上一动点(OC>1),连接BC,以线段BC为边在第四象限内作等边△CBD,直线DA交y轴于点E.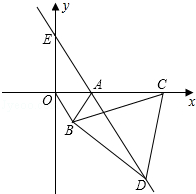
(1)△OBC与△ABD全等吗?判断并证明你的结论;
(2)随着点C位置的变化,点E的位置是否会发生变化?若没有变化,求出点E的坐标;若有变化,请说明理由.
阅读所给的材料,然后解答问题:如图①,在“格点”直角坐标系上我们可以发现:求线段DE的长度,可以转化为求Rt△DEF的斜边长,例如:在坐标系中我们发现:D(-7,5),E(4,-3),所以DF=|5-(-3)|=8,EF=|4-(-7)|=11,所以据勾股定理可得:DE=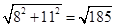 .
.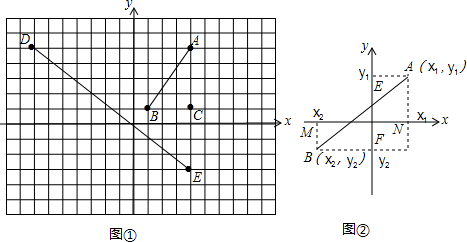
(1)在图①中用上面的方法可求出线段AB的长为 ;
(2)在图②中:设A(x1.y1),B(x2,y2),试用x1,x2,y1,y2表示:AC= ,BC= ,AB= ;
(3)已知A(2,1),B(4,3),试用(2)中得出的结论求线段AB的长;
(4)已知A(2,1),B(4,3),若点C为y轴上的点且使得△ABC是以AB为底边的等腰三角形,试求出点C的坐标.
某高校学生会向全校2900名学生发起了“爱心一日捐”捐款活动,为了解捐款情况,学生会随机调查了部分学生的捐款金额,并用得到的数据绘制了如下统计图①和图②,请根据相关信息,解答下列问题: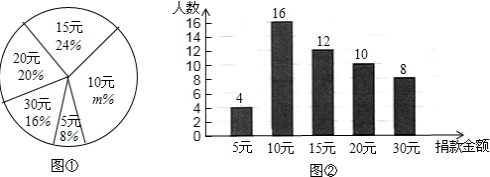
(1)本次接受随机抽样调查的学生人数为 ,图①中m的值是 ;
(2)求本次你调查获取的样本数据的平均数、众数和中位数;
(3)根据样本数据,估计该校本次活动捐款金额为10元的学生人数.
某酒店客房部有三人间、双人间客房,收费数据如下表.
为吸引游客,实行团体入住五折优惠措施.一个50人的旅游团优惠期间到该酒店入住,住了一些三人普通间和双人普通间客房.若每间客房正好住满,且一天共花去住宿费1510元,则旅游团住了三人普通间和双人普通间客房各多少间?
| 普通(元/间/天) |
豪华(元/间/天) |
|
| 三人间 |
150 |
300 |
| 双人间 |
140 |
400 |