如图,在矩形ABCD中,对角线BD的垂直平分线MN与AD相交于点M,与BC相交于点N,连接BM,DN.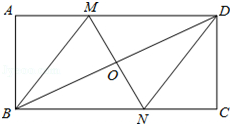
(1)求证:四边形BMDN是菱形;
(2)若AB=4,AD=8,求MD的长.
在直角坐标系中,设x轴为直线l,函数 的图像分别是
的图像分别是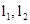 ,半径为1的
,半径为1的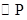 与直线
与直线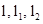 中的两条相切,例如
中的两条相切,例如 是其中一个
是其中一个 的圆心坐标.
的圆心坐标.
(1)写出其余满足条件的 的圆心坐标;
的圆心坐标;
(2)在图中标出所有圆心,并用线段依次连接各圆心,求所得几何图形的周长.
把一条12个单位长度的线段分成三条线段,其中一条线段长为4个单位长度,另两条线段长都是单位长度的整数倍.
(1)不同分法得到的三条线段能组成多少个不全等的三角形?用尺规作出这些三角形(用给定的单位长度,不写作法,保留作图痕迹);
(2)求出(1)中所作三角形外接圆的周长.
设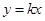 ,是否存在实数
,是否存在实数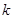 ,使得代数式
,使得代数式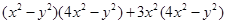 能化简为
能化简为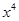 ?若能,请求出所有满足条件的
?若能,请求出所有满足条件的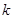 值,若不能,请说明理由.
值,若不能,请说明理由.
在
中,
,点
,
分别在
,
上,
,
与
相交于点
,求证:
,并请直接写出图中其他相等的线段.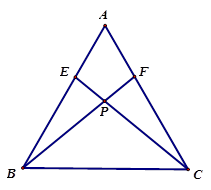
一个布袋中装有只有颜色不同的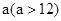 个球,分别是2个白球,4个黑球,6个红球和b个黄球,从中任意摸出一个球,把摸出白球,黑球,红球的概率绘制成统计图(未绘制完整),请补全该统计图并求出
个球,分别是2个白球,4个黑球,6个红球和b个黄球,从中任意摸出一个球,把摸出白球,黑球,红球的概率绘制成统计图(未绘制完整),请补全该统计图并求出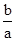 的值.
的值.