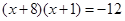如图,线段AB与⊙O相切于点C,连结OA,OB,OB交⊙O于点D,已知OA="OB=6" ,∠A=30°.

(1)求⊙O的半径;
(2)求图中阴影部分的面积.
已知:二次函数 的图象经过点
的图象经过点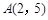 .
.
(1)求二次函数的解析式;
(2)求二次函数的图象与x轴的交点坐标;
(3)将(1)中求得的函数解析式用配方法化成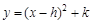 的形式.
的形式.
如图,甲、乙两人在玩转盘游戏时,准备了两个可以自由转动的转盘A,B,每个转盘被分成面积相等的几个扇形,并在每一个扇形内标上数字.游戏规则:同时转动两个转盘,当转盘停止后,指针所指区域的数字之和为0时,甲获胜;数字之和为1时,乙获胜.如果指针恰好指在分割线上,那么重转一次,直到指针指向某一区域为止.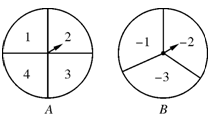
(1)用画树状图或列表法求乙获胜的概率;
(2)这个游戏规则对甲、乙双方公平吗?请判断并说明理由.
如图,点A、B的坐标分别为(0,0)、(4,0),将△ABC绕点A按逆时针方向旋转90º得到△AB′C′.
(1)画出△AB′C′;
(2)写出点C′的坐标.
运用适当的方法解方程(共16分)
(1)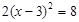
(2)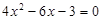
(3)
(4)