将一副三角尺如图拼接：含30°角的三角尺（△ABC）的长直角边与含45°角的三角尺（△ACD）的斜边恰好重合．已知AB＝2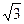
，P是线段AC上的一个动点．
（1）当点P运动到∠ABC的平分线上时，连结DP，求DP的长；
（2）当点P在运动过程中出现PD＝BC时，∠PDA= ；
（3）当PC= 时，以D，P，B，Q为顶点的平行四边形的顶点Q恰好在边BC上，
此时□DPBQ的面积= ．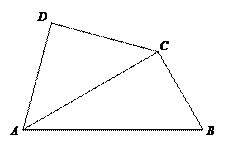
如图以O为圆心的两个同心圆，AB经过圆心O，且与小圆相交于点A，与大圆相交于点B，小圆的切线AC与大圆相交于点D，且OC平分∠ACB．
⑴试判断BC所在的直线与小圆的位置关系，并说明理由；
⑵试判断线段AC、AD、BC之间的数量关系，并说明理由；
⑶若AB＝8cm，BC＝10cm，求大圆与小圆围成的圆环的面积
如图，等腰梯形ABCD的底边AD在x轴上，顶点C在y轴正半轴上，B（4,2），一次函数y=kx-1的图象平分它的面积，关于x的函数y=mx2-(3m+k)x+2m+k的图象与坐标轴只有两个交点，求m的值.
用两个全等的正方形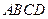
和
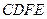拼成一个矩形
，把一个足够大的直角三角尺的直角顶点与这个矩形的边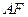
的中点
重合，且将直角三角尺绕点按逆时针方向旋转．
（1）当直角三角尺的两直角边分别与矩形
的两边
相交于点
时，如图甲，通过观察或测量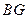
与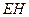
的长度，你能得到什么结论？并证明你的结论．（2）当直角三角尺的两直角边分别与
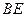的延长线，
的延长线相交于点时（如图乙），你在图甲中得到的结论还成立吗？简要说明理由．
先化简,再求值: 
,其中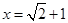
.
解方程.