随着人们经济收入的不断提高及汽车产业的快速发展,汽车已越来越多的进入普通家庭,成为居民消费新的增长点。据某市交通部门统计,2008年底全市汽车拥有量为15万辆,而截止到2010年底,全市的汽车拥有量已达21.6万辆。
求2008年底至2010年底该市汽车拥有量的年平均增长率;
(2)为了保护环境,缓解汽车拥堵状况,从2011年起,该市交通部门拟控制汽车总量,要求到2012年底全市汽车拥有量不超过23.196万辆;另据估计,该市从2011年起每年报废的汽车数量是上年底汽车拥有量的10%。假定在这种情况下每年新增汽车数量相同,请你计算出该市每年新增汽车数量最多不能超过多少万辆。
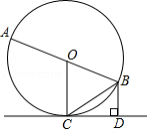
如图所示, 是 的直径,点 为 上一点,过点 作 ,垂足为点 ,连接 . 平分 .
求证: 为 的切线.
如图,抛物线 与两坐标轴相交于点 、 、 , 是抛物线的顶点, 是线段 的中点.
(1)求抛物线的解析式,并写出 点的坐标;
(2) 是抛物线上的动点:
①当 , 时,求 的面积的最大值;
②当 时,求点 的坐标.

如图, 、 是以 为直径的 上的点, ,弦 交 于点 .
(1)当 是 的切线时,求证: ;
(2)求证: ;
(3)已知 , 是半径 的中点,求线段 的长.

如图,已知四边形 中,对角线 、 相交于点 ,且 , ,过 点作 ,分别交 、 于点 、 .
(1)求证: ;
(2)判断四边形 的形状,并说明理由.

“绿水青山,就是金山银山”.某旅游景区为了保护环境,需购买 、 两种型号的垃圾处理设备共10台.已知每台 型设备日处理能力为12吨;每台 型设备日处理能力为15吨;购回的设备日处理能力不低于140吨.
(1)请你为该景区设计购买 、 两种设备的方案;
(2)已知每台 型设备价格为3万元,每台 型设备价格为4.4万元.厂家为了促销产品,规定货款不低于40万元时,则按9折优惠;问:采用(1)设计的哪种方案,使购买费用最少,为什么?