(本小题满分12分)
设 ,
,
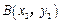 两点在抛物线
两点在抛物线 上,
上,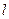 是
是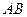 的垂直平分线.
的垂直平分线.
( 1)当且仅当
1)当且仅当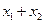 取何值时,直线
取何值时,直线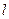 经过抛物线的焦点
经过抛物线的焦点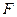 ?证明你的结论;
?证明你的结论;
(2)当直线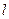 的斜率为2时,求
的斜率为2时,求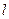 在
在 轴上截距的取值范围.
轴上截距的取值范围.
(本题满分14分)已知函数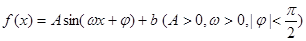 的一系列对应值如下表:
的一系列对应值如下表:
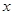 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
(1)根据表格提供的数据求函数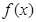 的解析式;
的解析式;
(2)根据(1)的结果,若函数 周期为
周期为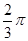 ,求
,求 在区间
在区间 上的最大、最小值及对应的
上的最大、最小值及对应的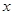 的值.
的值.
( 本题满分12分) 已知函数

(1)求 的最小正周期、单调增区间、对称轴和对称中心;
的最小正周期、单调增区间、对称轴和对称中心;
(2)该函数图象可由 的图象经过怎样的平移和伸缩变换得到?
的图象经过怎样的平移和伸缩变换得到?
(本题满分12分)已知: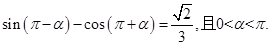 求下列各式的值:
求下列各式的值:
(1)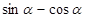 ; (2)
; (2)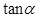 ; (3)
; (3)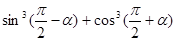
设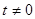 ,点P(
,点P(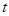 ,0)是函数
,0)是函数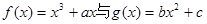 的图象的一个公共点,两函数的图象在点P处有相同的切线.
的图象的一个公共点,两函数的图象在点P处有相同的切线.
(Ⅰ)用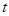 表示a,b,c;
表示a,b,c;
(Ⅱ)若函数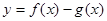 在(-1,3)上单调递减,求
在(-1,3)上单调递减,求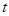 的取值范围.
的取值范围.
设函数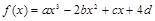 (a、b、c、d∈R)图象关于原点对称,且x=1时,
(a、b、c、d∈R)图象关于原点对称,且x=1时,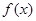 取极小值
取极小值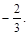
(1)求a、b、c、d的值;
(2)当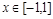 时,图象上是否存在两点,使得过此两点处的切线互相垂直?试证明你的结论;
时,图象上是否存在两点,使得过此两点处的切线互相垂直?试证明你的结论;
(3)若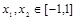 时,求证:
时,求证: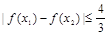 .
.