(本小题满分12分)若 时,不等式
时,不等式 恒成立,求a的取
恒成立,求a的取
值范围.
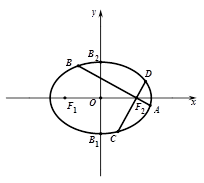
(本小题满分14分)如图所示,椭圆 的左右焦点分别为
的左右焦点分别为 ,点
,点 为椭圆
为椭圆 与坐标轴的交点,其中
与坐标轴的交点,其中 面积为
面积为 ,且椭圆
,且椭圆 的离心率为
的离心率为 .
.
(1)求椭圆 的方程;
的方程;
(2)过椭圆 的右焦点
的右焦点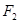 作两条相互垂直的弦
作两条相互垂直的弦 ,求由
,求由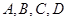 四点构成的四边形的面积的取值范围.
四点构成的四边形的面积的取值范围.
(本小题满分14分)设正数数列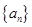 的前n项和为
的前n项和为 ,
,
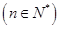 .
.
(1)求证: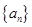 是等差数列;
是等差数列;
(2)设 为数列{
为数列{ }的前n项和,求
}的前n项和,求 ;
;
(3)设 ,证明:
,证明: 
(本小题满分14分)如图所示,平面
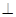 平面
平面 ,且四边形
,且四边形 为正方形,
为正方形, ,
, ∥
∥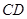 ,
, ,
, 为
为 的中点.
的中点.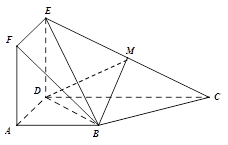
(1)求证: ∥平面
∥平面 ;
;
(2)求证: 平面
平面 ;
;
(3)求三棱锥 的体积.
的体积.
(本小题满分12分)广东某高中进行高中生歌唱比赛,在所有参赛成绩中随机抽取 名学生的成绩,按成绩分组:第
名学生的成绩,按成绩分组:第 组
组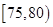 ,第
,第 组
组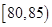 ,第
,第 组
组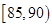 ,第
,第 组
组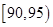 ,第
,第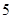 组
组 得到的频率分布直方图如图所示.现在组委会决定在笔试成绩高的第
得到的频率分布直方图如图所示.现在组委会决定在笔试成绩高的第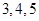 组中用分层抽样抽取
组中用分层抽样抽取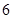 名学生进入第二轮面试.
名学生进入第二轮面试.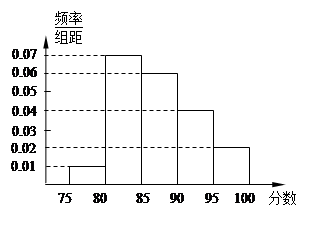
(1)求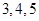 组各应抽取多少人进入第二轮面试;
组各应抽取多少人进入第二轮面试;
(2)学校决定在(1)中抽取的这6名学生中随机抽取2名学生接受考官D的面试,求第四组中至少一人被考官D面试的概率.
(本小题满分12分)已知函数
(1)求 取得最大值时,
取得最大值时,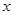 取值的集合与
取值的集合与 最大值
最大值
(2)若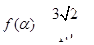 ,求
,求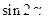 的值.
的值.