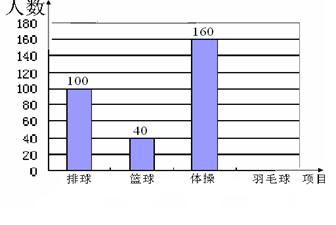
学校为了学生的身体健康，每天开展体育活动一小时，开设排球、篮球、羽毛
球、体操课．学生可根据自己的爱好任选其中一项，老师
根据学生报名情况进行了统计，并绘制了右边尚未完成的扇形统计图和频数分布直方图，请你结合图中的信息，解答下列问题：
（1）该校学生报名总人数有多少人？
（2）从表中可知选羽毛球的学生有多少人？选排球和篮球的人数分别占报名总人数的百分
之几？
（3）将两个统计图补充完整． 
如图，抛物线y=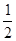
x2+bx－2与x轴交于A、B两点，与y 轴交于C点，且A（一1，0）．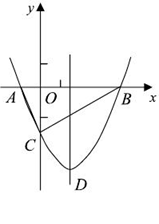
求抛物线的解析式及顶点D的坐标；
若将上述抛物线先向下平移3个单位，再向右平移2个单位，
请直接写出平移后的抛物线的解析式.
解不等式组
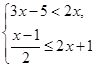
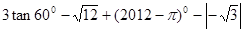
如图，在平面直角坐标系中，抛物线
经过A（3，0），B（0，－3）两点，点P是直线AB上一动点，过点P作
轴的垂线交抛物线于点M，设点P的横坐标为t，分别求直线AB和这条抛物线的解析式
若点P在第四象限，连结BM、AM，当线段PM最长时，求
的面积。
③是否存在这样的点P，使得以点P、M、B、O为顶点的四边形为平行四边形？若存在，请直接写出点P的横坐标；若不存在，请说明理由。
在直角梯形ABCD中，AB∥CD，∠ABC=900，AB=2BC=2CD，对角线AC与BD相交于点O，线段OA、OB的中点分别为点E、F求证：
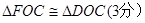
求
的值若直线EF与线段AD、BC分别相交于点G、H，求
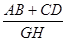的值