如图,AB是⊙O的直径,点D在AB的延长线上,点C在⊙O上, CA=CD,
∠ACD=120°.
(1)试探究直线CD与⊙O的位置关系,并说明理由;
(2)若BD为2.5,求△ACD中CD边的高.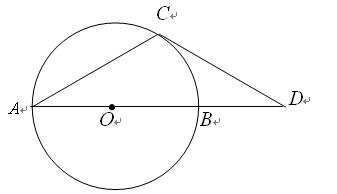
先化简,再求值: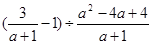 ,其中
,其中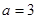
(1) 计算: 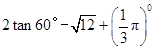 (2)解方程:
(2)解方程: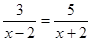
如图,在△ABC中,AB=AC=10cm,BD⊥AC于D,且BD=8cm.点M从点A出发,沿AC方向匀速运动,速度为2cm/s;同时直线PQ由点B出发沿BA方向匀速运动,速度为1cm/s,运动过程中始终保持PQ∥AC,直线PQ交AB于P,交BC于Q,连接PM,设运动时间为t(s)(0<t<5).
(1)当四边形PQCM是平行四边形时,求t的值;
(2)当t为何值时,△PQM是等腰三角形?
(3)以PM为直径作⊙E,在点P、Q整个运动过程中,是否存在这样的时刻t,使得⊙E与BC相切?若存在,请求出运动时间t的值;若不存在,请说明理由.
如图①,在矩形 ABCD中,AB=10cm,BC=8cm.点P从A出发,沿A→B→C→D路线运动,到D停止;点Q从D出发,沿 D→C→B→A路线运动,到A停止.若点P、点Q同时出发,点P的速度为每秒1cm,点Q的速度为每秒2cm,a秒时点P、点Q同时改变速度,点P的速度变为每秒bcm,点Q的速度变为每秒dcm.图②是点P出发x秒后△APD的面积S1(cm2)与x(秒)的函数关系图象;图③是点Q出发x秒后△AQD的面积S2(cm2)与x(秒)的函数关系图象.


(1)参照图象,求b、图②中c及d的值;
(2)连接PQ,当PQ平分矩形ABCD的面积时,运动时间x的值为;
(3)当两点改变速度后,设点P、Q在运动线路上相距的路程为y(cm),求y(cm)与运动时间x(秒)之间的函数关系式,并写出自变量x的取值范围;
(4)若点P、点Q在运动路线上相距的路程为25cm,求x的值.
如图,已知抛物线y=ax2+2x+c的顶点为A(―1,―4),与y轴交于点B,与x轴负半轴交于点C.
(1)求这条抛物线的函数关系式;
(2)点P为第三象限内抛物线上的一动点,连接BC、PC、PB,求△BCP面积的最大值,并求出此时点P的坐标;
(3)点E为抛物线上的一点,点F为x轴上的一点,若四边形ABEF为平行四边形,请直接写出所有符合条件的点E的坐标.