如图:抛物线顶点坐标为点C(1,4),交x轴于点A(3,0),交y轴于点B.
(1)求抛物线和直线AB的解析式;
(2)点Q(x,0)是x轴上的一动点,过Q点作x轴的垂线,交抛物线于P点、交直线BA于D点,连结OD,PB,当点Q(x,0)在x轴上运动时,求PD与x之间的函数关系式;四边形OBPD能否成为平行四边形,若能求出Q点坐标,若不能,请说明理由。
(3) 是否存在一点Q,使以PD为直径的圆与y轴相切,若存在,求出Q点的坐标;若不存 在,请说明理由.
在,请说明理由.

如图,在Rt△ABC中,∠BAC=90°,AB=AC,点D是△ABC内一点,连结AD,将线段AD绕点A逆时针旋转一定角度得到线段AE使∠BAD=∠CAE(E在AC右侧),连结BD,CE.
(1)求证:BD=CE;
(2)若AD=2,求点D绕点A旋转到点E所经过的路径长.
如表,给出了一个二次函数的一些取值情况:
(1)请在坐标系中(答卷纸上)画出这个二次函数的图象;
(2)根据图象写出:当0≤y<3时x的取值范围.
(1)计算: ;
;
(2)化简:
某自行车厂计划每天平均生产n辆自行车,而实际产量与计划产量相比有出入.下表记录了某周五个工作日每天实际产量情况(超过计划产量记为正、少于计划产量记为负):
| 星期 |
一 |
二 |
三 |
四] |
五 |
| 实际生产量 |
+5 |
﹣2 |
﹣4 |
+13 |
﹣3 |
(1)用含n的代数式表示本周前三天生产自行车的总数;
(2)该厂实行每日计件工资制,每生产一辆车可得60元,若超额完成任务,则超过部分每辆另奖15元;少生产一辆扣20元,当n=100时,那么该厂工人这一周的工资总额是多少元?
(3)若将上面第(2)问中“实行每日计件工资制”改为“实行每周计件工资制”,其他条件不变,当n=100时,在此方式下这一周工人的工资与按日计件的工资哪一个更多?请说明理由.
重百商场正销售某品牌的一款等离子宽屏幕电视机,年初时售价定为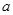 元,3月份售价降低了
元,3月份售价降低了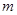 元.由于伦敦奥运会的举行,8月份销售看好,故商场决定将售价在3月份的基础上上涨10%.奥运会结束后,由于销售不畅,故商场决定将售价在8月份的基础上下调10%.
元.由于伦敦奥运会的举行,8月份销售看好,故商场决定将售价在3月份的基础上上涨10%.奥运会结束后,由于销售不畅,故商场决定将售价在8月份的基础上下调10%.
(1)请用代数式表示该款等离子宽屏幕电视机现在的价格;
(2)若年初时售价定为6500元,3月初售价降低了500元,那么该款等离子宽屏幕电视机现在的价格是多少元?