某班同学对南昌市市民对于“八一南昌起义”这件事的了解程度进行调查,他们将了解程度分为“清楚”、“了解”、“知道”“不知道”四级将调查结果绘制成以下统计表和条形统计图

(1) 这次调查的样本容量是 
(2)若将四种情况用扇形统计图表示,则“了解”和“知道”两种情况所对圆心角和为
度
(3)补充统计表和条形统计图
(4)若南昌市共有市民480万人,请你估计“清楚”这一事件的可能有多少人?
某电器超市销售每台进价分别为200元、170元的A、B两种型号的电风扇,下表是近两周的销售情况:
(进价、售价均保持不变,利润=销售收入﹣进货成本)
(1)求A、B两种型号的电风扇的销售单价;
(2)若超市准备用不多于5400元的金额再采购这两种型号的电风扇共30台,求A种型号的电风扇最多能采购多少台?
(3)在(2)的条件下,超市销售完这30台电风扇能否实现利润为1400元的目标?若能,请给出相应的采购方案;若不能,请说明理由.
学校为统筹安排大课间体育活动,在各班随机选取了一部分学生,分成四类活动:“篮球”、 “羽毛球”、 “乒乓球”、“其他”进行调查,整理收集到的数据,绘制成如下的两幅统计图.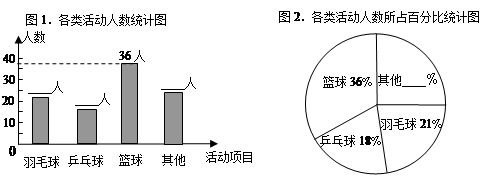
(1)学校采用的调查方式是;学校在各班共随机选取了名学生;
(2)补全统计图中的数据:羽毛球人、乒乓球人、其他人、其他﹪;
(3)该校共有1100名学生,请计算喜欢“篮球”的学生人数.
已知:如图,在平行四边形ABCD中,O为对角线BD的中点,过点O的直线EF分别交AD,BC于E,F两点,连结BE,DF.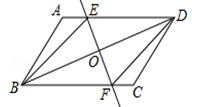
(1)求证:OE=OF.
(2)当∠DOE等于度时,四边形BFDE为菱形.(直接填写答案即可)
在边长为1的小正方形网格中,△AOB的顶点均在格点上.
(1)B点关于y轴的对称点坐标为;
(2)将△AOB向左平移3个单位长度得到△A1O1B1,请画出△A1O1B1;
(3)在(2)的条件下,A1的坐标为.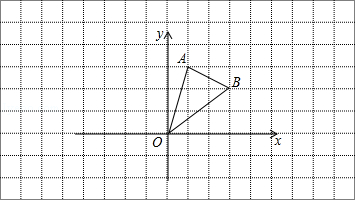
化简: