(8分)问题情景：某学校数学学习小组在讨论“随机掷二枚均匀的硬币，得到一正一反的概率是多少”时，小聪说：随机掷
二枚均匀的硬币，可以有“二正、一正一反、二反”三种情况，所以，P（一正一反）＝
；小颖反驳道：这里的“一正一反”实际上含有“一正一反，一反一正”二种情况，所以P（一正一反）＝
.
⑴ 的说法是正确的.
⑵为验证二人的猜想是否正确，小聪与小颖各做了100次实验，得到如下数据：
计算：小聪与小颖二人得到的“一正一反”的频率分别是多少？从他们的实验中，你能得
到“一正一反”的概率是多少吗？
⑶对概率的研究而言小聪与小颖两位同学的实验说明了什么？
某县为了了解“十、一”国庆期间该县常住居民的出游情况，有关部门随机调查了1600名常住居民，并根据调查结果绘制了如下统计图：
 |
根据以上信息，解答下列各题：
(1)补全条形统计图，在扇形统计图中，直接填入出游主要目的是采集发展信息的人数的百分数；
(2)若该县常住居民共48万人，请估计该县常住居民中，利用“十、一”期间出游采集发展信息的人数；
(3)综合上述信息，用一句话谈谈你的感想.
．已知：如图4，在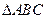
中，∠BAC=90°，DE、DF是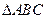的中位线，连结EF、AD.求证：EF=AD．
（1）先化简，再求值：
(2)已知一次函数y=kx+b的图像经过两点A(1,1)，B(2,-1)，求这个函数的解析式．
如图5，在A岛周围25海里水域有暗礁，一轮船由西向东航行到O处时，发现A岛在北偏东
°方向，轮船继续前行20海里到达B处发现A岛在北偏东
方向，该船若不改变航向继续前进，有无触
礁的危险？ （参考数据：
）
(10分)如图，已知抛物线与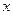
轴交于A(1，0)，B（
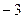，0）两点，与
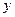轴交于点
C(0，3)，抛物线的顶点为P，连结AC．
(1)求此抛物线的解析式；
(2)在抛物线上找一点D，使得DC与AC垂直，且直线DC与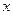轴交于点Q，求点D的坐标；
(3)抛物线对称轴上是否存在一点M，使得S△MAP=2S△ACP，若存在，求出M点坐标；若不存在，请说明理由．