(本题满分10分)如图,直角梯形ABCD中,AD∥BC,∠A=90°,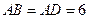 ,
,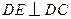 交AB于E,DF平分∠EDC交BC于F,连结
交AB于E,DF平分∠EDC交BC于F,连结 EF.
EF.
(1)证明: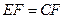
 ;
;
(2)当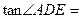
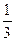 时,求EF的长.
时,求EF的长.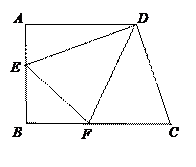
如图,二次函数 的图象与x轴交于A、B 两点,与y轴交于点C,且点B的坐标为(1,0),点C的坐标为(0,﹣3),一次函数y2=mx+n的图象过点A、C.
的图象与x轴交于A、B 两点,与y轴交于点C,且点B的坐标为(1,0),点C的坐标为(0,﹣3),一次函数y2=mx+n的图象过点A、C.
(1)求二次函数的解析式;
(2)求二次函数的图象与x轴的另一个交点A的坐标;
(3)根据图象写出y2<y1时,x的取值范围.
阅读材料,解答问题.
例用图象法解一元二次不等式:.x2﹣2x﹣3>0
解:设y=x2﹣2x﹣3,则y是x的二次函数.∵a=1>0,∴抛物线开口向上.
又∵当y=0时,x2﹣2x﹣3=0,解得x1=﹣1,x2=3.
∴由此得抛物线y=x2﹣2x﹣3的大致图象如图所示.
观察函数图象可知:当x<﹣1或x>3时,y>0.
∴x2﹣2x﹣3>0的解集是:x<﹣1或x>3.
(1)观察图象,直接写出一元二次不等式:x2﹣2x﹣3>0的解集是 ;
(2)仿照上例,用图象法解一元二次不等式:x2﹣1>0.
已知:二次函数y=﹣x2+2x+3
(1)求抛物线的对称轴和顶点的坐标;
(2)画出函数图象;
(3)根据图象:
①写出函数值y为正数时,自变量x的取值范围;
②写出当﹣2<x<2时,函数值y的取值范围.
二次函数y=ax2+bx+c(a≠0)的图象如图所示,根据图象解答下列问题:
(1)写出方程ax2+bx+c=0的两个根;
(2)写出不等式ax2+bx+c>0的解集;
(3)写出y随x的增大而减小的自变量x的取值范围;
(4)若方程ax2+bx+c=k有两个不相等的实数根,求k的取值范围.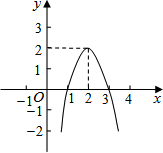
(1)请在坐标系中画出二次函数y=x2﹣2x的大致图象;
(2)根据方程的根与函数图象的关系,将方程x2﹣2x=1的根在图上近似的表示出来(描点);
(3)观察图象,直接写出方程x2﹣2x=1的根.(精确到0.1)