已知如图,矩形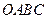 的长
的长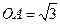 ,宽
,宽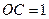 ,将
,将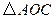 沿
沿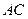 翻折得
翻折得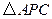 .
.
(1)填空: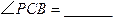 度,
度,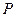 点坐标为( , );
点坐标为( , );
(2)若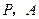 两点在抛物线
两点在抛物线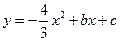 上,求
上,求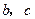 的值,并说明点
的值,并说明点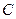 在此抛物线上;
在此抛物线上;
(3)在(2)中的抛物线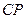 段(不包括
段(不包括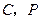 点)上,是否存在一点
点)上,是否存在一点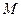 ,使得四边形
,使得四边形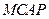 的面积最大?若存在,求出这个最大值及此时
的面积最大?若存在,求出这个最大值及此时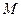 点的坐标;若不存在,请说明理由.
点的坐标;若不存在,请说明理由.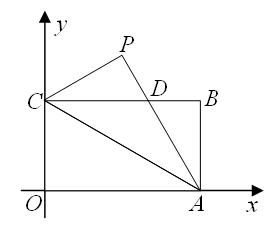
(满分8分)漳州市教育局到某校抽查七年级学生 “根据音标写单词”的水平,随机抽取若干名学生进行测试(成绩取整数,满分为100分).如下两幅是尚未绘制完整的统计图,请根据图中提供的信息,解答下列问题:
(1)本次抽取的学生有人;
(2)该年段有450名学生,若全部参加测试,请估计60分以上(含60分)有人;
(3)甲、乙、丙是该校三名英语成绩优秀的学生,随机抽取其中两名学生介绍英语学习经验,请用树状图或列表法表示所有可能的结果,并求抽到甲、乙两名学生的概率.
(满分8分)动手操作:
用两种不同的方法,将下图中一个等腰三角形分割成四个等腰三角形.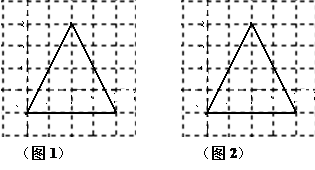
(满分8分)如图:O是正方形ABCD对角线的交点,圆心角为90°的扇形EOF从图1位置,顺时针旋转到图2位置, 、
、 分别交
分别交 、
、 于
于 、
、 .\
.\
(1)猜想AG与BH的数量关系;
(2)证明你的猜想.
(满分8分)请从以下三个二元一次方程: x+y=7,  , x+3y=11中,任选两个方程构成一个方程组,并解该方程组.
, x+3y=11中,任选两个方程构成一个方程组,并解该方程组.
(1)所选方程组是:.
(2)解方程组:
在平面直角坐标系中,横坐标与纵坐标都为整数的点叫整点,动点P从原点O出发,运动速度为每秒1个单位长度,规定P只能向上或向右运动,请回答下列问题:
(1)填表
| 运动时间(秒) |
可得到的整点坐标 |
整点个数 |
 |
||
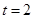 |
||
 |
(2)当t=12时,整点有个
(3)当t=时,可得到整点(8,7)
(4)当t=时,可得到整点(m,n)