如图①已知△ABC中，AB=BC=1，∠ABC=90°，把一块含30°角的三角板DEF的直角顶点D放在AC的中点上（直角三角板的短直角边为DE，长直角边为DF），将直角三角板DEF绕D点按逆时针方向旋转。
（1）在图①中，DE交A
B于M，DF交BC于N，①证明：DM=DN；②在这一过程中，直角三角板DEF与△ABC的重叠部分DMBN，请说明四边形DMBN的面积是否发生变化，若发生变化，请说明四边形DMBN如何变化。若不变，求其面积。
（2）继续旋转至如图②延长AB交DE于M，延长BC交DF于N，DM=DN是否仍然成立？若成立请给出证明；若不成立，请说明理由？
（3）继续转至图③延长FD交BC于N延长ED交AB于M，DM=DN是否仍然成立？若成立请直接写出结论，不用证明。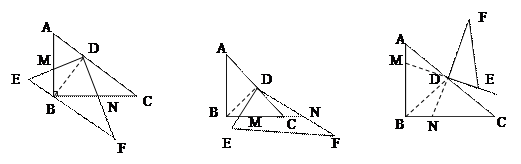
① ② ③
为了解某校九年级全体男生1000米跑步的成绩，随机抽取了部分男生进行测试，并将测试成绩分为 A、 B、 C、 D四个等级，绘制如下不完整的统计图表，如图表所示，根据图表信息解答下列问题：
成绩等级频数分布表
|
成绩等级 |
频数 |
|
A |
24 |
|
B |
10 |
|
C |
x |
|
D |
2 |
|
合计 |
y |
（1） x＝ ， y＝ ，扇形图中表示 C的圆心角的度数为 度；
（2）甲、乙、丙是 A等级中的三名学生，学校决定从这三名学生中随机抽取两名介绍体育锻炼经验，用列表法或画树状图法，求同时抽到甲，乙两名学生的概率．
如图，在△ ABC中，点 D是 AB边上的一点．
（1）请用尺规作图法，在△ ABC内，求作∠ ADE，使∠ ADE＝∠ B， DE交 AC于 E；（不要求写作法，保留作图痕迹）
（2）在（1）的条件下，若 ＝2，求 的值．
已知在平面直角坐标系中，点 A（3，0）， B（﹣3，0）， C（﹣3，8），以线段 BC为直径作圆，圆心为 E，直线 AC交⊙ E于点 D，连接 OD．
（1）求证：直线 OD是⊙ E的切线；
（2）点 F为 x轴上任意一动点，连接 CF交⊙ E于点 G，连接 BG；
①当tan∠ ACF＝ 时，求所有 F点的坐标 （直接写出）；
②求 的最大值．
如图抛物线 y＝ ax 2+ bx+ c经过点 A（﹣1，0），点 C（0，3），且 OB＝ OC．
（1）求抛物线的解析式及其对称轴；
（2）点 D、 E在直线 x＝1上的两个动点，且 DE＝1，点 D在点 E的上方，求四边形 ACDE的周长的最小值．
（3）点 P为抛物线上一点，连接 CP，直线 CP把四边形 CBPA的面积分为3：5两部分，求点 P的坐标．
有 A、 B两个发电厂，每焚烧一吨垃圾， A发电厂比 B发电厂多发40度电， A焚烧20吨垃圾比 B焚烧30吨垃圾少1800度电．
（1）求焚烧1吨垃圾， A和 B各发电多少度？
（2） A、 B两个发电厂共焚烧90吨的垃圾， A焚烧的垃圾不多于 B焚烧的垃圾两倍，求 A厂和 B厂总发电量的最大值．