设数列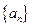 前
前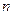 项和为
项和为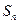 ,且
,且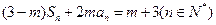 。其中
。其中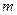 为实常数,
为实常数, 且
且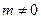 。
。
(1)求证: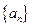 是等比数列;
是等比数列;
(2)若数列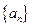 的公比满足
的公比满足 且
且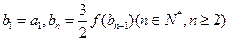 ,求
,求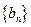 的
的
通项公式;
(3)若 时,设
时,设 ,是否存在最大的正整数
,是否存在最大的正整数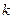 ,使得对任意
,使得对任意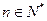 均有
均有 成立,若存在求出
成立,若存在求出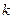 的值,若不存在请说明理由。
的值,若不存在请说明理由。
已知数列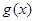 的前n项和为
的前n项和为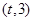 ,
,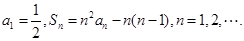
(1)证明:数列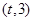 是等差数列,并求
是等差数列,并求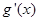 ;
;
(2)设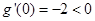 ,求证:
,求证: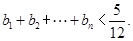
已知函数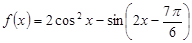 .
.
(1)求函数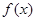 的最大值,并写出
的最大值,并写出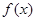 取最大值时
取最大值时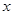 的取值集合;
的取值集合;
(2)已知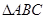 中,角
中,角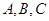 的对边分别为
的对边分别为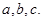 若
若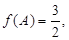
 求实数
求实数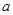 的最小值.
的最小值.
已知f(x)=|x+1|+|x-1|,不等式f(x)的解集为M.
(1).求M;
(2).当a,b M时,证明:2|a+b|<|4+ab|.
M时,证明:2|a+b|<|4+ab|.
以直角坐标系的原点为极点O, 轴正半轴为极轴,已知点P的直角坐标为(1,-5),点C的极坐标为
轴正半轴为极轴,已知点P的直角坐标为(1,-5),点C的极坐标为 ,若直线l经过点P,且倾斜角为
,若直线l经过点P,且倾斜角为 ,圆C的半径为4.
,圆C的半径为4.
(1).求直线l的参数方程及圆C的极坐标方程;
(2).试判断直线l与圆C有位置关系.
如图,四边形为边长为a的正方形,以D为圆心,DA为半径的圆弧与以BC为直径的圆O交于F,连接CF并延长交AB于点E.
(1).求证:E为AB的中点;
(2).求线段FB的长.