(本小题满分14分)已知直线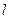 :kx-y-3k=0;圆M:
:kx-y-3k=0;圆M: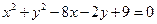
(Ⅰ)求证:直线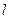 与圆M必相交;
与圆M必相交;
(Ⅱ)当圆M截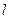 所得弦最长时,求k的值。
所得弦最长时,求k的值。
(本小题满分12分)
某班主任为了解所带班学生的数学学习情况,从全班学生中随机抽取了20名学生,对他们的数学成绩进行统计,统计结果如图.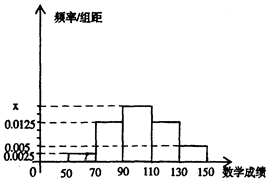
 (Ⅰ)求x的值和数学成绩在110分以上的人数;
(Ⅰ)求x的值和数学成绩在110分以上的人数;
(Ⅱ)从数学成绩在110分以上的学生中任意抽 取3人,成绩在130分以上的人数为ξ,求ξ的期望.
取3人,成绩在130分以上的人数为ξ,求ξ的期望.
(本小题满分12分)
在△ABC中,a、b、c分别是角A、B、C的对边,且(2a+c)cosB+bcosC=0.
(Ⅰ)求角B 的值;
的值;
(Ⅱ)已知函数f(x)=2cos(2x-B),将f(x)的图象向左平移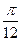 后得到函数g(x)的图象,求g(x)的单调增区间.
后得到函数g(x)的图象,求g(x)的单调增区间.
12分)设等比数列 的首项
的首项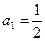 ,
, 前n项和为
前n项和为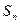 ,且
,且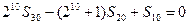 ,且数列
,且数列 各项均正。
各项均正。
(1)求 的通项;
的通项;
(2)求 的前n项和
的前n项和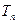 。
。
.已知数列 的前n项和为
的前n项和为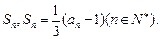
(1)求 ;
;
(2)求证数列 是等比数列。
是等比数列。
(12分)
一缉私艇发现在北偏东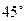 方向,距离12 nmile的海面上有一走私船正以10 nmile/h的速度沿东偏南
方向,距离12 nmile的海面上有一走私船正以10 nmile/h的速度沿东偏南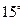 方向逃窜.缉私艇的速度为14 nmile/h, 若要在最短的时间内追上该走私船,缉私艇应沿北偏东
方向逃窜.缉私艇的速度为14 nmile/h, 若要在最短的时间内追上该走私船,缉私艇应沿北偏东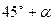 的方向去追,.求追上所需的时间和
的方向去追,.求追上所需的时间和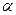 角的正弦值.
角的正弦值.