(本小题满分14分)
如图,在四棱锥 中,底面ABCD是正方形,侧棱
中,底面ABCD是正方形,侧棱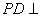 底面ABCD,
底面ABCD,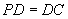 ,E是PC的中点,作
,E是PC的中点,作 交PB于点F;
交PB于点F;
(I)证明  平面
平面 ;
;
(II)证明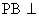 平面EFD;
平面EFD;
(本题满分15分)已知函数f(x)=(2-a)(x-1)-2lnx,,其中a∈R,
(1)求f(x)的单调区间;
(2)若函数f(x)在(0,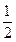 )上无零点,求a的取值范围.
)上无零点,求a的取值范围.
(本题满分14分)设点F(0,2),曲线C上任意一点M(x,y)满足以线段FM为直径的圆与x 轴相切.
(1)求曲线C的方程;
(2)设过点Q(0,-2)的直线l与曲线C交于A,B两点,问|FA|,|AB|,|FB|能否成等差数列?若能,求出直线l的方程;若不能,请说明理由.
(本题满分15分)圆C过点A(2,0)及点B( ,
, ),且与直线l:y=
),且与直线l:y= 相切
相切
(1)求圆C的方程;
(2)过点P(2,1)作圆C的切线,切点为M,N,求|MN|;
(3)点Q为圆C上第二象限内一点,且∠BOQ= ,求Q点横坐标.
,求Q点横坐标.
(本题满分14分)△ABC中,已知角A、B、C的对边分别为a、b、c,若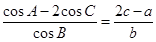 .
.
(1)求 的值;
的值;
(2)若b=2,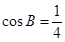 ,求△ABC的面积S.
,求△ABC的面积S.
(本题满分14分) 已知集合A={x|x2-2x-3≤0},B={x|x2-2mx+m2-4≤0}
(1)若A∩B=[1,3],求实数m的值;
(2)若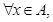 都有
都有 ,求实数m的取值范围.
,求实数m的取值范围.