已知命题
：方程
表示焦点在
轴上的椭圆；命题
：实数
使得不等式
成立．
（1）若
时，求命题中的椭圆的离心率；
（2）求命题是命题的什么条件．
某村计划建造一个室内面积为800平米的矩形蔬菜温室，在温室内沿左右两侧与后墙内侧各保留1米的通道，沿前侧内墙保留3米宽的空地，当矩形温室的边长各为多少时，蔬菜的种植面积最大？最大的种植面积是多少？
已知椭圆C的短轴的一个端点为(0,1)，离心率为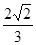
．
⑴求该椭圆的方程；
⑵设直线y=x+2交椭圆C于A、B两点，求线段AB的长。
设数列{
}的前n项和
=n2，{
}为等比数列，且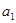
=
，
(
-)=．
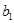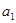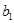⑴求数列{}和{}的通项公式；
⑵求数列{}的前n项和。
若一个动点P(x,y)到两个定点A(-1，0)、B(1，0)的距离差的绝对值为定值2a,求点P的轨迹方程，并说明轨迹的形状.
给定两个命题，p：对任意实数x都有ax2+ax+1>0恒成立；q：关于x的方程x2-x+a=0有实数根。如果p∨q为真命题，p∧q为假命题，求实数a的取值范围