(理科)已知函数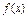 =x2-4x+a+3,g(x)=mx+5-2m.
=x2-4x+a+3,g(x)=mx+5-2m.
(Ⅰ)若y=f(x)在[-1,1]上存在零点,求实数a的取值范围;
(Ⅱ)当a=0时,若对任意的x1∈[1,4],总存在x2∈[1,4],使f(x1)=g(x2)成立,求实数m的取值范围;
(Ⅲ)若函数y=f(x)(x∈[t,4])的值域为区间D,是否存在常数t,使区间D的长度为7-2t?若存在,求出t的值;若不存在,请说明理由(注:区间[p,q]的长度为q-p).
从某节能灯生产在线随机抽取100件产品进行寿命试验,按连续使用时间(单位:天)共分5组,得到频率分布直方图如图.
(I)以分组的中点资料作为平均数据,用样本估计该生产线所生产的节能灯的预期连续使用寿命;
(II)为了分析使用寿命差异较大的产品,从使用寿命低于200天和高于350天的产品中用分层抽样的方法共抽取6件,求样品A被抽到的概率。
已知数列 为等差数列,且
为等差数列,且
(1)求数列 的通项公式;
的通项公式;
(2)证明 …
… .
.
已知 中,
中, 是三个内角
是三个内角 的对边,关于
的对边,关于 的
的
不等式 的解集是空集。
的解集是空集。
(1)求角 的最大值;
的最大值;
(2)若 ,
, 的面积
的面积 ,求当角
,求当角 取最大值时
取最大值时 的值。
的值。
已知向量 ,
, =(
=( ,
, ),记
),记 ;
;
(1)若 ,求
,求 的值;
的值;
(2)若 中,角
中,角 的对边分别是
的对边分别是 ,且满足
,且满足 ,求函数
,求函数 的取值范围.
的取值范围.
在海岸 处,发现北偏东
处,发现北偏东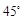 方向,距
方向,距 为
为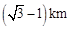 的
的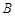 处有一艘走私船,在
处有一艘走私船,在 处北偏西
处北偏西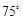 方向,距
方向,距 为
为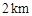 的
的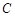 处的缉私船奉命以
处的缉私船奉命以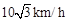 的速度追截走私船,此时走私船正以
的速度追截走私船,此时走私船正以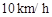 的速度从
的速度从 处向北偏东
处向北偏东 方向逃窜,问缉私船沿什么方向能最快追上走私船,并求出所需要的时间. (
方向逃窜,问缉私船沿什么方向能最快追上走私船,并求出所需要的时间. (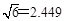 )
)