(本小题满分14分)如图,在直三棱柱ABC-A1B1C1中,点D、E分别在边BC、
B1C1上,CD=B1E=AC,ÐA CD=60°.
CD=60°.
求证:(1)BE∥平面AC1D;
(2) 平面ADC1⊥平面BCC1B1.
平面ADC1⊥平面BCC1B1.

已知函数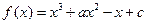 ,且
,且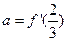 .
.
(1)求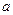 的值;
的值;
(2)求函数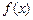 的单调区间;
的单调区间;
(3)设函数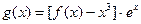 ,若函数
,若函数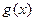 在
在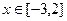 上单调递增,求实数
上单调递增,求实数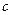 的取值范围.
的取值范围.
已知椭圆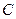 的中心在坐标原点,焦点在
的中心在坐标原点,焦点在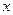 轴上,离心率为
轴上,离心率为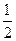 ,椭圆
,椭圆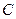 上的点到焦点距离的最大值为
上的点到焦点距离的最大值为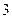 .
.
(1)求椭圆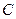 的标准方程;
的标准方程;
(2)若过点 的直线
的直线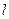 与椭圆
与椭圆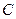 交于不同的两点
交于不同的两点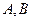 ,且
,且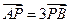 ,求实数
,求实数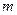 的取值范围.
的取值范围.
已知曲线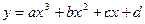 满足下列条件:
满足下列条件:
①过原点;②在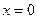 处导数为-1;③在
处导数为-1;③在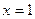 处切线方程为
处切线方程为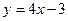 .
.
(1) 求实数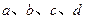 的值;
的值;
(2)求函数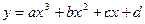 的极值.
的极值.
已知双曲线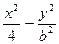 ="1"
="1" 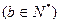 的两个焦点为
的两个焦点为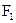 、
、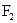 ,P是双曲线上的一点,
,P是双曲线上的一点,
且满足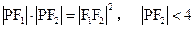 ,
,
(1)求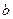 的值;
的值;
(2)抛物线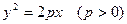 的焦点F与该双曲线的右顶点重合,斜率为1的直线经过点F与该抛物线交于A、B两点,求弦长|AB|.
的焦点F与该双曲线的右顶点重合,斜率为1的直线经过点F与该抛物线交于A、B两点,求弦长|AB|.
证明以下不等式:
(1)已知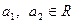 ,
,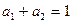 ,求证:
,求证: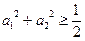 ;
;
(2)若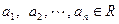 ,
,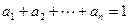 ,求证:
,求证: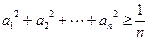 .
.