(本小题满分16分)经销商用一辆J型卡车将某种水果从果园运送(满载)到相距400km的水果批发市场.据测算,J型卡车满载行驶时,每100km所消耗的燃油量u(单位: 资、车损等其他费用平均每小时300元.已知燃油价格为每升(L)7.5元.
资、车损等其他费用平均每小时300元.已知燃油价格为每升(L)7.5元.
(1)设运送这车水果 的费用为y(元)(不计返程费用),将y表示成速度v的函数
的费用为y(元)(不计返程费用),将y表示成速度v的函数 关系式;
关系式;
(2)卡车该以怎样的速度行驶,才能使运送这车水果的费用最少?
(本小题满分12分)如下图,给出了一个程序框图,其作用是输入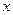 的值,输出相应的
的值,输出相应的 的值,
的值,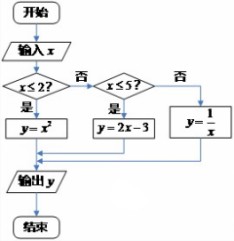
(I)请指出该程序框图所使用的逻辑结构;
(Ⅱ)若视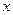 为自变量,
为自变量, 为函数值,试写出函数
为函数值,试写出函数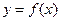 的解析式;
的解析式;
(Ⅲ)若要使输入的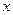 的值与输出的
的值与输出的 的值相等,求输入
的值相等,求输入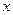 的值的集合
的值的集合
(本小题满分12分)某中学生物兴趣小组在学校生物园地种植了一批名贵树苗,为了解树苗的生长情况,从这批树苗中随机地测量了其中50棵树苗的高度(单位:厘米),并把这些高度列成了如下的频数分布表:
(1)在这批树苗中,其高度在85厘米以上的树苗大约有多少棵?
(2)这批树苗的平均高度大约是多少?;
(3)为了进一步获得研究资料,若从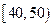 组中移出一棵树苗,从
组中移出一棵树苗,从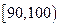 组中移出两棵树苗进行试验研究,则
组中移出两棵树苗进行试验研究,则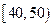 组中的树苗A和
组中的树苗A和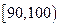 组中的树苗C同时被移出的概率是多少?
组中的树苗C同时被移出的概率是多少?
(本小题满分12分 )已知实数
)已知实数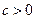 ,设P:函数
,设P:函数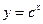 在R上单调递减,
在R上单调递减,
Q:关于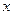 的一元二次方程
的一元二次方程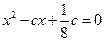 有两个不相等的实数根,
有两个不相等的实数根,
如果命题“ ”为真命题,命题“
”为真命题,命题“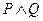 ”为假命题,求实数
”为假命题,求实数 的取值范围.
的取值范围.
设函数
(1)若
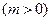 上的最大值
上的最大值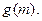
(2)若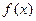 在区间[1,2]上为减函数,求a的取值范围。
在区间[1,2]上为减函数,求a的取值范围。
(3)若直线 为函数
为函数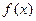 的图象的一条切线,求a的值。
的图象的一条切线,求a的值。
设直线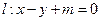 与抛物线
与抛物线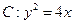 交于不同两点A、B,F为抛物线的焦点。
交于不同两点A、B,F为抛物线的焦点。
(1)求 的重心G的轨迹方程;
的重心G的轨迹方程;
(2)如果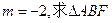 的外接圆的方程。
的外接圆的方程。