小明和小刚用如图所示的两个转盘做游戏,游戏规则如下:分别旋转两个转盘,当两个转盘所转到的数字之积为奇数时,小明得2分;当所转到的数字之积为偶数时,小刚得1分。这个游戏对双方公平吗?若公平,说明理由。若不公平,如何修改规则才能使游戏对双方公平?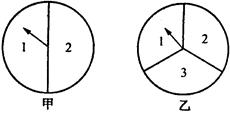
已知关于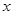 的一元二次方程为
的一元二次方程为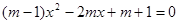 .
.
(1)试说明此方程有两个不相等的实数根;
(2)当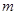 为何整数时,此方程的两个根都为正整数?
为何整数时,此方程的两个根都为正整数?
某校体育组为了了解学生喜欢的体育项目,从全校同学中随机抽取了若干名同学进行调查,每位同学从兵乓球、篮球、羽毛球、排球、跳绳中选择一项最喜欢的项目,并将调查的结果绘制成如下的两幅统计图.根据以上统计图,解答下列问题: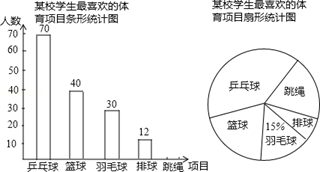
(1)这次抽样调查中,共调查了名学生;
(2)补全条形统计图,并求扇形统计图中表示“乒乓球”的扇形的圆心角度数;
(3)若全校有1500名同学,估计全校最喜欢篮球的有多少名同学?
先化简,再求值:( +
+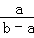 )÷
)÷ ,其中a,b满足
,其中a,b满足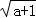 +|b﹣
+|b﹣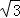 |=0.
|=0.
已知 是方程
是方程 的一个实数根,则代数式
的一个实数根,则代数式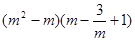 的值为.
的值为.
如图,对称轴为直线x=-1的抛物线y=x2+bx+c与x轴相交于A、B两点,与y轴的交于C点,其中A点的坐标为(-3,0).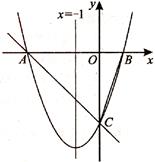
(1)求抛物线的表达式;
(2)若将此抛物线向右平移m个单位,A、B、C三点在坐标轴上的位置也相应的发生移动,在移动过程中,△BOC能否成为等腰直角三角形?若能,求出m的值,若不能,请说明理由.