在科技馆里,小亮看见一台名为帕斯卡三角的仪器,如图所示,当一实心小球从入口落下,它在依次碰到每层菱形挡块时,会等可能地向左或向右落下.
(1)试问小球通过第二层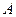 位置的概率是多少?
位置的概率是多少?
(2)请用学过的数学方法模拟试验,并具体说明小球下落到第三层 位置和第四层
位置和第四层
位置处的概率各是多少? 解:
解:
某中学为了解某年级1200名学生每学期参加社会实践活动时间,随机对该年级50名学生进行了调查,结果如下表:
| 时间(天) |
4 |
5 |
6 |
7 |
8 |
9 |
10 |
11 |
12 |
13 |
| 人数 |
1 |
2 |
4 |
5 |
7 |
11 |
8 |
6 |
4 |
2 |
(1)在这个统计中,众数是 ,中位数是 ;
(2)补全下面的频率分布表和频率分布直方图:
| 分组 |
频数 |
频率 |
| 3.5~5.5 |
3 |
0.06 |
| 5.5~7.5 |
9 |
0.18 |
| 7.5~9.5 |
0.36 |
|
| 9.5~11.5 |
14 |
|
| 11.5~13.5 |
6 |
0.12 |
| 合计 |
50 |
1.00 |

(3)请你估算这所学校该年级的学生中,每学期参加社会实践活动时间不少于9天的大约有多少人?
如图, 是⊙O的直径,
是⊙O的直径,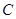 为
为 延长线上的一点,
延长线上的一点,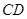 交⊙O于点
交⊙O于点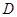 ,且
,且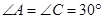 .
.
(1)求证: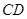 是⊙O的切线;
是⊙O的切线;
(2)请直接写出图中某3条线段之间的等量关系式,只要写出3个。(添加的辅助线不能用)
解方程: 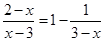
计算: 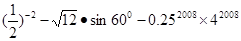
已知二次函数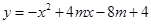 :
:
(1) 证明:当m为整数时,抛物线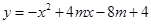 与x轴交点的横坐标均为整数;
与x轴交点的横坐标均为整数;
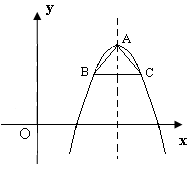
(2) 以抛物线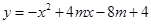 的顶点A为等腰Rt△的直角顶点,作该抛物线的内接等腰Rt△ABC(B、C两点在抛物线上),求Rt△ABC的面积(图中给出的是m取某一值时的示意图);
的顶点A为等腰Rt△的直角顶点,作该抛物线的内接等腰Rt△ABC(B、C两点在抛物线上),求Rt△ABC的面积(图中给出的是m取某一值时的示意图);
(3) 若抛物线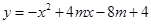 与直线y=7交点的横坐标均为整数,求整数m的值.
与直线y=7交点的横坐标均为整数,求整数m的值.