在如图所示的平面直角坐标系中,直线AB:y=k1x+b1与直线AD:y=k2x+b2相交于点A(1,3),且点B坐标为(0,2),直线AB交x轴负半轴于点C,直线AD交x轴正半轴于点D.
(1)求直线AB的函数解析式;
(2)根据图象直接回答,不等式k1x+b1<k2x+b2的解集;
(3)若△ACD的面积为9,求直线AD的函数解析式;
(4)若点M为x轴一动点,当点M在什么位置时,使AM+BM的值最小?求出此时点M的坐标.
计算: .
.
如图,在平面直角坐标系中,直线 分别交
分别交 轴,
轴, 轴于
轴于 两点,以
两点,以 为边作矩形
为边作矩形 ,
, 为
为 的中点.以
的中点.以 ,
, 为斜边端点作等腰直角三角形
为斜边端点作等腰直角三角形 ,点
,点 在第一象限,设矩形
在第一象限,设矩形 与
与 重叠部分的面积为
重叠部分的面积为 .
.
求点
 的坐标;
的坐标;当
 值由小到大变化时,求
值由小到大变化时,求 与
与 的函数关系式;
的函数关系式;若在直线
 上存在点
上存在点 ,使
,使 等于
等于 ,请直接写出
,请直接写出 的取值范围
的取值范围在
 值的变化过程中,若
值的变化过程中,若 为等腰三角形,且PC=PD,请直接写出
为等腰三角形,且PC=PD,请直接写出 的值.
的值.
如图,在直角坐标平面内,函数 (
(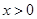 ,
,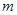 是常数)
是常数)
的图象经过 ,
, ,其中
,其中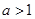 .过点
.过点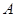 作
作 轴垂线,
轴垂线,
垂足为 ,过点
,过点 作
作 轴垂线,垂足为
轴垂线,垂足为 ,连结
,连结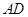 ,
, ,
, .
.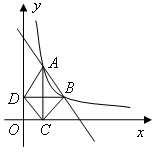
若
 的面积为4,求点
的面积为4,求点 的坐标;
的坐标;若
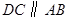 ,当
,当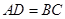 时,求直线
时,求直线 的函数的解析式.
的函数的解析式.
在长方形中画出5条线,把它分成的块数与画线的方式有直接关系.按如图1的方式画线,可以把它分成10块.请你在图2中画出5条线,使得把这个长方形分成的块数最少(重合的线只看做一条),最少可分成块;
请你在图2中画出5条线,使得把这个长方形分成的块数最多,最多可分成块.
(画出图形不写画法和理由)
如图,在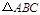 中,
中, ,以AB为直径的
,以AB为直径的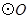 交BC
交BC
于点D,DE⊥AC于点E.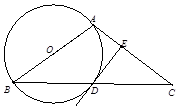
求证DE是
 的切线;
的切线;若∠BAC=120°,AB=2,求△DEC的面积.