﹣(本题12分)甲船从A港出发顺流匀速驶向B港,行至某处,发现船上一救生圈不知何时落入水中,立刻原路返回,找到救生圈后,继续顺流驶向B港.乙船从B港出发逆流匀速驶向A港.已知救生圈漂流的速度和水流速度相同;甲、乙两船在静水中的速度相同.甲、乙两船到A港的距离y1、y2(km)与行驶时间x(h)之间的函数图象如图所示.
(1)写出乙船在逆流中行驶的速度.
(2)求甲船在逆流中行驶的路程.
(3)求甲船到A港的距离y1与行驶时间x之间的函数关系式.
(4)求救生圈落入水中时,甲船到A港的距离.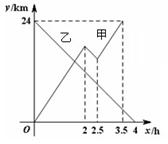 【参考公式:船顺流航行的速度
【参考公式:船顺流航行的速度 船在静水中航行的速度+水流速度,船逆流航行的速度
船在静水中航行的速度+水流速度,船逆流航行的速度 船在静水中航行的速度
船在静水中航行的速度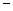 水流速度.】
水流速度.】