直线 与反比例函数
与反比例函数 的图象相交于点
的图象相交于点 、
、 ,
, 与
与 轴交于点
轴交于点 ,其中点
,其中点 的坐标为
的坐标为 ,点
,点 的横坐标为
的横坐标为 .
.
(1)试确定反比例函数的关系式.
(2)求 的面积.
的面积.
(3)如图直接写出反比例函数值大于一次函数值的自变量 的取值范围.
的取值范围.
解不等式组: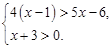
如图,已知直线l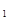 ∥l
∥l ,一个45°角的顶点A在l
,一个45°角的顶点A在l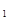 上,过A作AD⊥l
上,过A作AD⊥l ,垂足为D,AD=6.将这个角绕顶点A旋转(角的两边足够长).
,垂足为D,AD=6.将这个角绕顶点A旋转(角的两边足够长).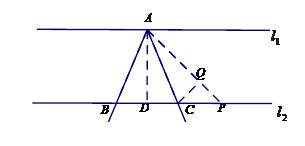

(1)如下图,旋转过程中,若角的两边与l 分别交于B、C,且AB=AC,求BD的长.
分别交于B、C,且AB=AC,求BD的长.
为了解决这个问题,下面提供一种解题思路:如图,作∠DAP=45°,AP与l 相交于点P,过点C作CQ⊥AP于点Q.∵∠DAP=∠BAC =45°,∴∠BAD=∠CAQ, 请你接下去完成解答.
相交于点P,过点C作CQ⊥AP于点Q.∵∠DAP=∠BAC =45°,∴∠BAD=∠CAQ, 请你接下去完成解答.
(2)旋转过程中,若角的两边与l 分别交于E、F(E在F左面),且AE>AF,DF= 2,求DE的长.请你借鉴(1)的做法在备用图中画图并解答这个问题.
分别交于E、F(E在F左面),且AE>AF,DF= 2,求DE的长.请你借鉴(1)的做法在备用图中画图并解答这个问题.
如图,已知直线y=- x+2与坐标轴交于A、B两点,抛物线y=-
x+2与坐标轴交于A、B两点,抛物线y=-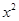 +bx+c与x轴交于A、C两点,与y轴交于点B.
+bx+c与x轴交于A、C两点,与y轴交于点B.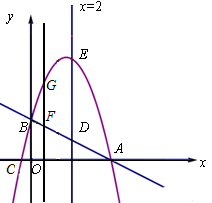
(1)求b、c的值.
(2)平行于y轴的直线x=2交直线AB于点D,交抛物线于点E.
①点P从原点O出发,沿x轴正方向以1个单位/秒的速度运动,设运动时间为t,过点P作x轴的垂线与直线AB交于点F,与抛物线交于点G,当t为何值时,FG∶DE=1∶2?
②将抛物线向上平移m(m>0)个单位后与y轴相交于点B′,与直线x=2相交于点E′,当E′O平分∠B′E′D时,求m的值.
如图1,在平面直角坐标系中,已知点A(-6,0),点B(0,8),点C在y轴上,将△OAB沿直线AC对折,使点O落在边AB上的点D处.
(1)求直线AB、AC的解析式.
(2)如图2,过B作BE⊥AC,垂足为E,若F为AB边上一动点,是否存在点F,使C为△EOF内心,若存在,请求出F点坐标,若不存在,请说明理由.
如图,已知扇形AOB中,∠AOB=120°,弦AB=2 ,点M是弧AB上任意一点(与端点A、B不重合),ME⊥AB于点E,以点M为圆心、ME长为半径作⊙M, 分别过点A、B作⊙M的切线,两切线相交于点C.
,点M是弧AB上任意一点(与端点A、B不重合),ME⊥AB于点E,以点M为圆心、ME长为半径作⊙M, 分别过点A、B作⊙M的切线,两切线相交于点C.
(1)求弧AB的长;
(2)试判断∠ACB的大小是否随点M的运动而改变,若不变,请求出∠ACB的大小;若改变,请说明理由.