如图,已知扇形AOB中,∠AOB=120°,弦AB=2 ,点M是弧AB上任意一点(与端点A、B不重合),ME⊥AB于点E,以点M为圆心、ME长为半径作⊙M, 分别过点A、B作⊙M的切线,两切线相交于点C.
,点M是弧AB上任意一点(与端点A、B不重合),ME⊥AB于点E,以点M为圆心、ME长为半径作⊙M, 分别过点A、B作⊙M的切线,两切线相交于点C.
(1)求弧AB的长;
(2)试判断∠ACB的大小是否随点M的运动而改变,若不变,请求出∠ACB的大小;若改变,请说明理由.
为了保护环境,某企业决定购买10台污水处理设备,现有A.B两种型号的设备,其中每台的价格.月处理污水量及年消耗费如下表:
| A型 |
B型 |
|
| 价格(万元/台) |
12 |
10 |
| 处理污水量(吨/月) |
240 |
200 |
| 年消耗费(万元/台) |
1 |
1 |
经预算,该企业购买设备的资金不高于105万元。
(1)请你设计该企业有几种购买方案;
(2)若企业每月产生的污水量为2040吨,为了节约资金,应选择哪种购买方案;
(3)在第(2)问的条件下,若每台设备的使用年限10年,污水厂处理污水费为每吨10元,请你计算,该企业自己处理污水与将污水排到污 水厂处理相比较,10年节约资金多少万元?(注:企业处理污水的费用包括购买设备的资金和消耗费)
水厂处理相比较,10年节约资金多少万元?(注:企业处理污水的费用包括购买设备的资金和消耗费)
解不等式组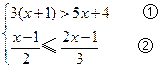 ,并将解集在数轴上表示出来.
,并将解集在数轴上表示出来. 22.
22.
解不等式组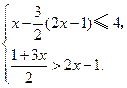 把解集表示在数轴上,并求
把解集表示在数轴上,并求 出不等式组的整数
出不等式组的整数
 如图,△ABC是一块
如图,△ABC是一块 锐角三角形余料,边BC=
锐角三角形余料,边BC= 120mm, 高AD=80mm, 要把它加
120mm, 高AD=80mm, 要把它加 工成矩形零件,使一边在BC上,其余两个顶点分别在边AB、AC上,
工成矩形零件,使一边在BC上,其余两个顶点分别在边AB、AC上,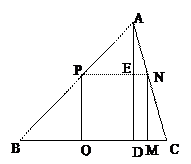
(1)若这个矩形是正方形,那 么边长是多少?
么边长是多少?
(2)若这个矩形的长是宽的2倍,则边长是多少?
在△ABC中,AE∶EB="1" ∶2,EF∥BC,AD∥BC交CE的延长线于D,求S△AEF∶S△BCE的值.