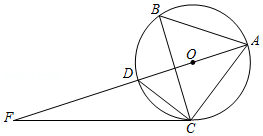
如图, 是 的外接圆, 是 的直径, 是 延长线上一点,连接 , ,且 .
(1)求证: 是 的切线;
(2)若 , ,求 的长.
某公司需将一批材料运往工厂,计划租用甲、乙两种型号的货车,在每辆货车都满载的情况下,若租用30辆甲型货车和50辆乙型货车可装载1500箱材料;若租用20辆甲型货车和60辆乙型货车可装载1400箱材料.
(1)甲、乙两种型号的货车每辆分别可装载多少箱材料?
(2)经初步估算,公司要运往工厂的这批材料不超过1245箱.计划租用甲、乙两种型号的货车共70辆,且乙型货车的数量不超过甲型货车数量的3倍,该公司一次性将这批材料运往工厂共有哪几种租车方案?
某校为了了解本校学生每天课后进行体育锻炼的时间情况,在5月份某天随机抽取了若干名学生进行调查,调查发现学生每天课后进行体育锻炼的时间都不超过100分钟,现将调查结果绘制成两幅尚不完整的统计图表.请根据统计图表提供的信息,解答下列问题:
|
组别 |
锻炼时间(分 |
频数(人) |
百分比 |
|
|
|
12 |
|
|
|
|
|
|
|
|
|
18 |
|
|
|
|
6 |
|
|
|
|
3 |
|
(1)本次调查的样本容量是 ;表中 , ;
(2)将频数分布直方图补充完整;
(3)已知 组有2名男生和1名女生,从中随机抽取两名学生,恰好抽到1名男生和1名女生的概率是 ;
(4)若该校学生共有2200人,请根据以上调查结果估计:该校每天课后进行体育锻炼的时间超过60分钟的学生共有多少人?

如图,一次函数 的图象与反比例函数 的图象相交,其中一个交点的横坐标是1.
(1)求 的值;
(2)若将一次函数 的图象向下平移4个单位长度,平移后所得到的图象与反比例函数 的图象相交于 , 两点,求此时线段 的长.

尺规作图(只保留作图痕迹,不要求写出作法).如图,已知 ,且 .
(1)在 边上求作点 ,使 ;
(2)在 边上求作点 ,使 .
